DAA-Assignment-1

Question 1

Given the input A=[11, -7, 8, 12, 6, 5, -6, 3] , track the divide-and-conquer algorithm to find the maximum contiguous subarray. You need to show the recursive calls as a tree. The input and output for each recursive call should also be indicated as well.

• Input: A=[11, -7, 8, 12, 6, 5, -6, 3]
• Output: MCS of A

\begin{algorithm}
	\caption{Maximum Contiguous Subarray Problem}
	\begin{algorithmic}
		\If{$i = j$}
    	\State \Return $R[i]$
	\Else
	    \State $s1 \gets \text{MCS}(R, i, \lfloor(i+j)/2\rfloor)$ \Comment{Using floor function for lower rounding}
	    \State $s2 \gets \text{MCS}(R, \lfloor(i+j)/2\rfloor + 1, j)$
	    \State $A \gets \text{MaxSuffix}(R, i, \lfloor(i+j)/2\rfloor) + \text{MaxPrefix}(R, \lfloor(i+j)/2\rfloor + 1, j)$
	    \State \Return $\text{MAX}(s1, s2, A)$
	\EndIf
	\end{algorithmic}
\end{algorithm}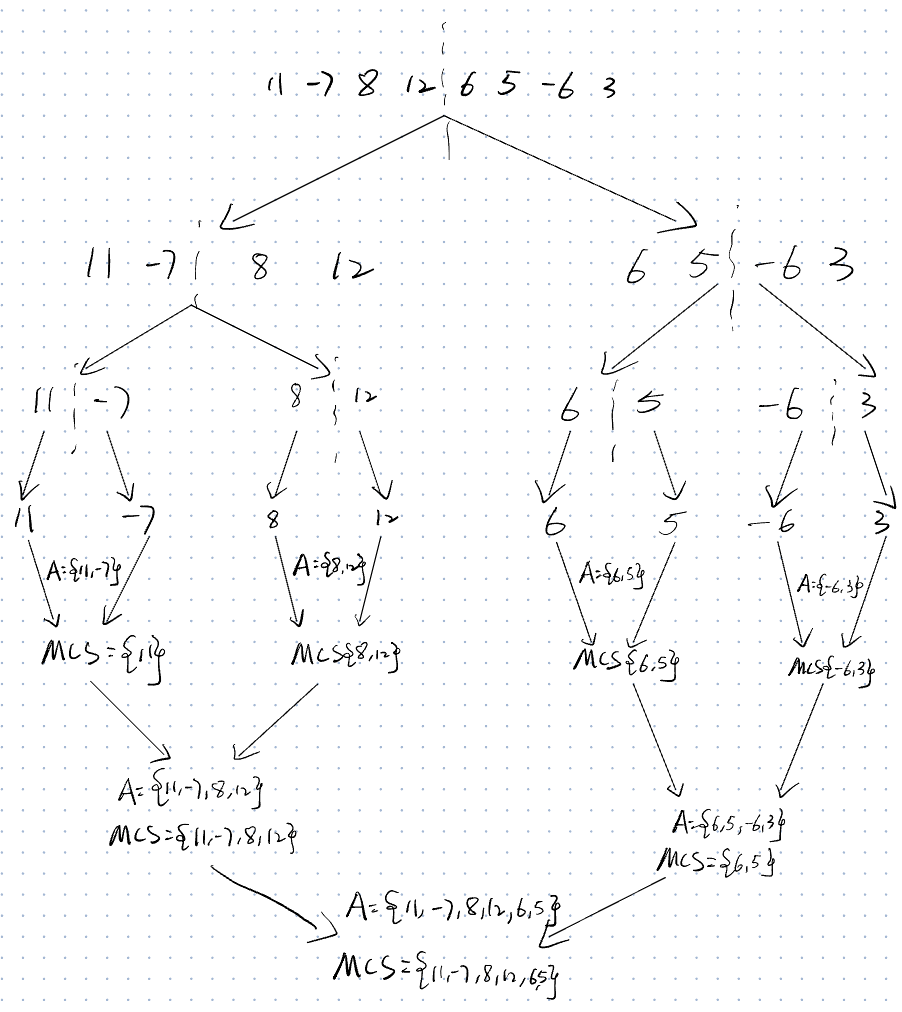

Question 2

Given two polynomials $A(x)=1+3x+x^3$ and $B(x)=2x+2x^2+x^4$, track the $O(n^{log3})$ algorithm to calculate $A(x)\times B(x)$. You need to show the recursive calls as a tree. The input and output for each recursive call should also be indicated as well.

• Input: Two polynomials A(X) and B(x) of order n
• Output: The polynomial C(X) = A(x)B(x)

   \usepackage{amsmath}
   \begin{algorithm}
   	\caption{Polynomial Multi2($A(x),B(x)$)}
       \begin{algorithmic}
   		\IF{$n=0$}
   		    \RETURN $a_0 \times b_0$
   		\ELSE
       		\STATE $A_0(x) = a_0 + a_1x + \dots + a_{\lfloor \frac{n}{2} \rfloor - 1}x^{\lfloor \frac{n}{2} \rfloor -1}$
   	    	\STATE $A_1(x) = a_{\lfloor \frac{n}{2} \rfloor} + a_{\lfloor \frac{n}{2} \rfloor +1}x + \dots + a_nx^{n-\lfloor \frac{n}{2} \rfloor}$
   	    	\STATE $B_0(x) = b_0 + b_1x + \dots + b_{\lfloor \frac{n}{2} \rfloor - 1}x^{\lfloor \frac{n}{2} \rfloor -1}$
   	    	\STATE $B_1(x) = b_{\lfloor \frac{n}{2} \rfloor} + b_{\lfloor \frac{n}{2} \rfloor +1}x + \dots + b_nx^{n-\lfloor \frac{n}{2} \rfloor}$
   	    	\STATE $Y(x) = \text{PolyMult2}(A_0(x)+A_1(x), B_0(x)+B_1(x))$
   	    	\STATE $U(x) = \text{PolyMult2}(A_0(x), B_0(x))$
   	    	\STATE $Z(x) = \text{PolyMult2}(A_1(x), B_1(x))$
   	    	\RETURN $U(x) + (Y(x) - U(x) - Z(x))x^{\lfloor \frac{n}{2} \rfloor} + Z(x)x^{2\lfloor \frac{n}{2} \rfloor}$
   		\ENDIF
   	\end{algorithmic}	
   \end{algorithm}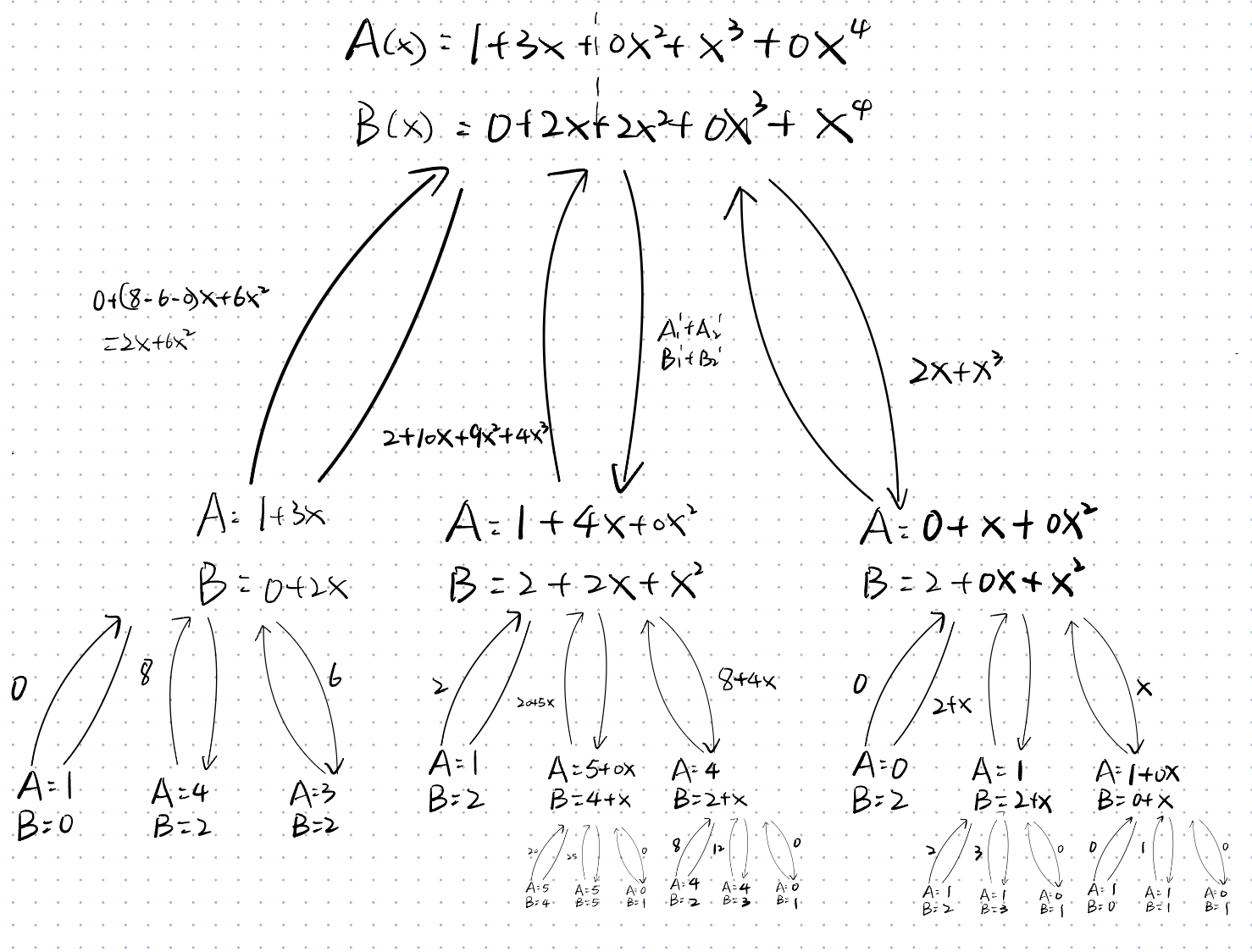

$$2x+6x^2+(x+10x+9x^2+4x^3-2x-x^3-2x-6x^2)x^2+(2x+x^3)x^4$$$$=2x+6x^2+2x^2+6x^3+3x^4+3x^5+2x^5+x^7$$$$=2x+8x^2+6x^3+3x^4+5x^5+x^7$$

---

---

---

---

Question 3

In the deterministic linear-time divide-and-conquer algorithm taught in class for the selection problem, the input array is divided into groups of 5 elements. Analyze the running time of the algorithm if the input array is divided into groups of 7. Does your algorithm run in linear time?

The Algorithm is still run in linear time

	\usepackage{amsmath}
    \begin{algorithm}
		\caption{Deterministic-Select($A,p,r,i$)}
	    \begin{algorithmic}
			\IF{$p=r$}
			    \RETURN $A[p]$
			\ENDIF
	    	\STATE $q = Deterministic-Partition(A,p,r)$
	    	\STATE $k = q - p + 1$
		    \IF{$i = k$}
			    \RETURN $A[q]$
			\ENDIF
			\IF{$i < k$}
			    \RETURN $Deterministic-Select(A,p,q-1,i)$
			\ENDIF
		    \IF{$i > k$}
			    \RETURN $Deterministic-Select(A,q+1,r,i-k)$
			\ENDIF
		\end{algorithmic}	
    \end{algorithm}

$$T(n)=\{\begin{array}{ll}O(1)& ifnissmall\\ O(n)+T(\lceil \frac{n}{7}\rceil )+max(T(Left+1),T(Right))\end{array}$$

Assume always Deterministic-Select Right (wlog)

$$|left|\ge 4(\frac{1}{2}\lceil \frac{n}{7}\rceil )$$$$|right|\le n-|left|=\frac{5n}{7}$$$$\therefore T(n)\le O(n)+T(\lceil \frac{n}{7}\rceil )+T\left(\frac{5n}{7}\right)\le O(n)+T(\frac{n}{7}+1)+T(\frac{5n}{7})$$

*Proof * $$T(n)=O(n)$$ Let $c=14a$ if a is large enough; $n_0=14$

$$\mathrm{\forall }n\ge n_{0}T(n)\le 14a\cdot n$$

By strong inductionBase case: When $$n=n_0=14$$ *Assume for all * $$n_{0}\leq k \leq n-1$$

$$T(k)\le 14a\cdot k$$

Goal $$T(n)\leq 14a\cdot n$$

$T(n)\le cn+T(\frac{n}{7}+1)+T(\frac{5n}{7})$$=cn+14a(\frac{n}{7}+1)+14a\cdot (\frac{5n}{7})$$=(c+14a\frac{6}{7})n+14a\le 14an$

---

---

---

---

---

---

---

Question 4

A segment  is a pair of positive integers $(a,b)$, where $(0<a<b)$. Two segments $s_1=(a_1,b_1)$ and $s_2=(a_2,b_2)$ intersect if $a_1<a_2<b_1<b_2$ .

Given a sequence  of  $s_1,s_2,...,s_n$ of $n$ segments sorted increasingly by $a$’s ($a_i\le a_j$  if $1\le i\le j\le n$ ) within the  r ($b_i\le r$  for all $1\le i\le n$), design a divide-and-conquer algorithm to justify if there are two segments intersect.

Describe your algorithm in a high-level presentation.

• Input:
  • Segments a sequence  of  $s_1,s_2,...,s_n$ of $n$ segments sorted increasingly by $a$’s ($a_i\le a_j$  if $1\le i\le j\le n$ ) within the  r ($b_i\le r$  for all $1\le i\le n$)
  • Left to indicate left endpoint
  • Right to indicate right endpoint
  • R to indicate r ($b_i\le r$  for all $1\le i\le n$)
• Output:
  • Boolean value indicating whether there is at least one pair of intersecting segments.

1. If the left and right indexes coincide, the intersect cannot be found. Return false;
2. Divide the array into two halves: the left sublist and the right sublist.
3. Recursively apply the algorithm to the left sublist to check for intersections.
4. Recursively apply the algorithm to the right sublist to check for intersections.
5. If any recursive call finds an intersection, return 'true' because we have already found the intersecting segments.
6. Otherwise look for MaxLeftB in the left sublist and MinRightA in the right list
7. If MinRightA is less than MaxLeftB, intersect is found
8. Otherwise return 'false'.

---

Write down the pseudo code.

\usepackage{amsmath}
\usepackage{algorithm}
\usepackage{algorithmic}

\begin{algorithm}
\caption{Check for Intersection in Segments}
\begin{algorithmic}

\FUNCTION{DoesIntersect}{$Segments$, $Left$, $Right$, $R$}
    \IF{$Left \geq Right$}
        \RETURN \textbf{false}
    \ENDIF
    \STATE $Mid \gets \lfloor(Left + Right) / 2\rfloor$
    \STATE $LeftIntersect \gets$ \CALL{DoesIntersect}{$Segments$, $Left$, $Mid$, $R$}
    \STATE $RightIntersect \gets$ \CALL{DoesIntersect}{$Segments$, $Mid + 1$, $Right$, $R$}
    \IF{$LeftIntersect$ \textbf{or} $RightIntersect$}
        \RETURN \textbf{true}
    \ENDIF
    \STATE $MaxLeftB \gets$ \CALL{FindMaxB}{$Segments$, $Left$, $Mid$}
    \STATE $MinRightA \gets$ \CALL{FindMinA}{$Segments$, $Mid + 1$, $Right$}
    \IF{$MaxLeftB > MinRightA$}
        \RETURN \textbf{true}
    \ENDIF
    \RETURN \textbf{false}
\ENDFUNCTION

\Function{FindMaxB}{$Segments, Left, Mid$} 
\State $MaxB \gets -\infty$ \For{$i \gets Left$ \textbf{to} $Mid$} \State $MaxB \gets \max(MaxB, Segments[i].b)$ \EndFor \State \Return $MaxB$ 
\EndFunction

\Function{FindMinA}{$Segments, Mid, Right$} \State $MinA \gets \infty$ \For{$i \gets Mid + 1$ \textbf{to} $Right$} \State $MinA \gets \min(MinA, Segments[i].a)$ \EndFor \State \Return $MinA$ \EndFunction

\end{algorithmic}
\end{algorithm}

---

---

Analyze the time complexity of your algorithm.

$$T(n)=\{\begin{array}{ll}O(1)& n=1\\ O(1)+O(n)+2T\left(\frac{n}{2}\right)& n>1\end{array}$$

When $n>1$

$$T(n)=O(1)+O(n)+2\cdot T(\frac{n}{2})$$$$T(\frac{n}{2})=O(1)+O(\frac{n}{2})+2\cdot T(\frac{n}{4})$$$$T(n)=3\cdot O(1)+2\cdot O(n)+4\cdot (T(\frac{n}{4}))$$$$T(n)=2^{m-1}\cdot O(1)+m\cdot O(n)+2^m\cdot (T(\frac{n}{2^m}))$$

When $n=2^m$

$$m=lo{g}_{2}n$$$$T(n)=(n-1)\cdot O(1)+{\log }_{2}n\cdot O(n)+n\cdot (O(1))$$$$T(n)=O(n)+O(n{\log }_{2}n)$$$$T(n)=O(n\log n)$$

---

Question 5

Assume: The number of terms in the polynomials is always an integer power of $2$

In other words, $n+1=2^1$ for some $i\ge 0$

Define a method  to convert polynomials in general to polynomials whose number of terms is an integer power of 2.

• If the number of terms of the polynomial is not a power of two
• Then by adding the number of terms to the polynomial until the number of terms becomes a power of two, the coefficient of the added term is 0

---

Discuss the consequence by doing so. Does it increase the time complexity comparing to the original algorithm? Why?

Hint: please pay attention to the input size

• Input: Two polynomials $A(x)$ and $B(x)$ of order $n$
• Output: The polynomials $C(x)=A(x)B(x)$

\begin{algorithm}
	\caption{PolyMulti(A(x),B(x))}
	\begin{algorithmic}
		\State \State $A^{'}(x)=M(A(x))$
	    \State $B^{'}(x)=M(B(x))$
		\RETURN GPolyMultic($A^{'}(x),B^{'}(x)$)
	\end{algorithmic}
\end{algorithm}

It will not increase the time complexity comparing to the original algorithm. The time cost will slightly increase. Suppose there are 2 polynomials with $n=2^{m-1}+1$ terms. After the operation it now turn to $2^m=2n-2$ terms. In original algorithm the time complexity is $O(n^{lo{g}_{2}3})$ Now the time complexity is $O((2n-2{)}^{lo{g}_{2}3})$ There are almost the same time complexity $O(n^{lo{g}_{2}3})$

---