CG-Assignment-2
Question-1
Give a sequence of 4x4 matrices that transforms the parallelogram in the left figure to the unit square in the right. Write down the name of the transformation for each matrix. Also write down the transformation matrix of each step.
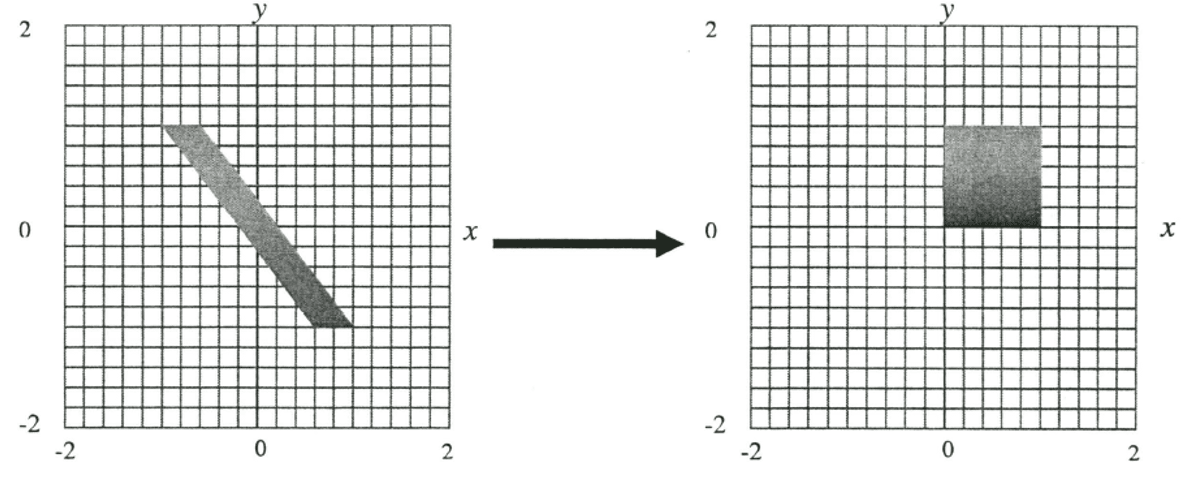
Firstly,Translate the parallelogram to the origin. The translation matrix is:
Then sheared the parallelogram to a rectangle. The shear matrix is:
Finally, scale the rectangle to a unit square. The scale matrix is:
The final transformation matrix is the product of the three matrices:
Question-2
The following converts an oblique frustum into an orthogonal one where the z-axis coincides with the frustum’s central line. Note that
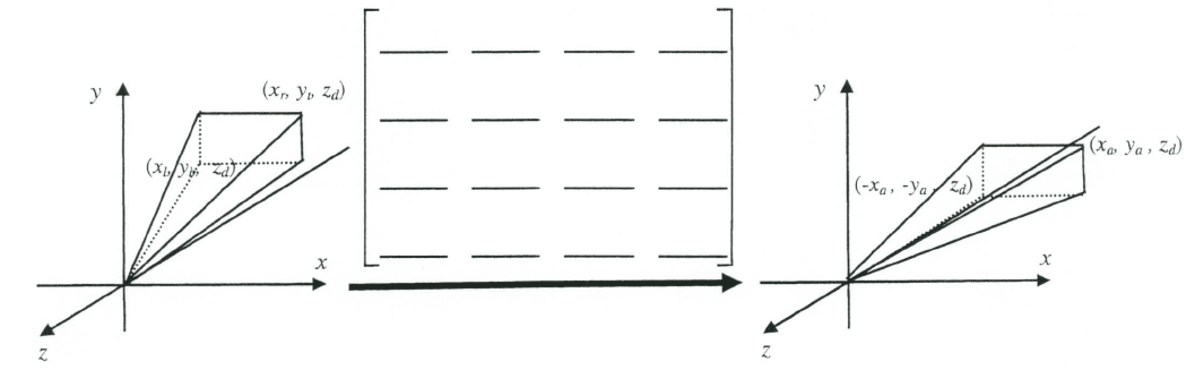
To transform the oblique frustum into an orthogonal frustum, we use a shear transformation matrix that aligns the centerline with the
- Original frustum coordinates:
- Right-top:
, - Left-bottom:
.
- Right-top:
- New orthogonal frustum:
- Right-top:
, - Left-bottom:
, where and .
- Right-top:
Shear Factors: To remove the offsets caused by the oblique frustum:
Shear Transformation Matrix:
Question-3
Consider the figure below. i is the direction of the incident light, n is the normal of the surface at S and r is the direction of the reflection. All of them are unit vectors. Derive a formula for r in terms of i and n.
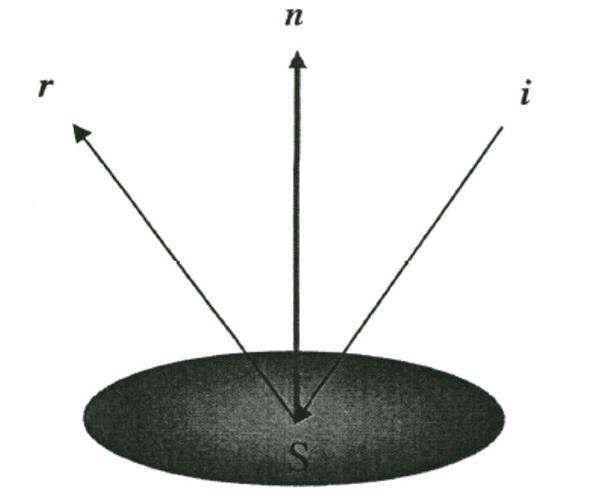
Decompose the incident vector
where:
(component parallel to the normal), (component perpendicular to the normal).
When reflected:
- The parallel component
is reversed: , - The perpendicular component
stays the same.
So the reflected vector becomes:
Substitute
Simplify:
Question-4
(a)
Derive the
To derive the homogeneous
Normalize the Direction Vector
Compute
Outer Product
Plug into Rodrigues' Formula Substitute into the formula for rotation, with
, , .
Compute Each Term
:
:
:
Add Terms Together Sum the above three terms to get:
Create the
Embed the
(b)
What is the image of point
The image of the point
Question-5
(a)
Given a triangle
- Affine Combination: Any point
in the plane of can be written as: because define the plane (not collinear). To ensure lies in the affine subspace of the triangle:
- Coordinate Representation: Let
, , , and . Write: with . This forms a system of linear equations to uniquely determine .
- Uniqueness: Assume
has two representations: Subtract: Since are not collinear (linearly independent), the only solution is:
Therefore, any point
(b)
To show that
Sufficient Condition (
): If and , is a convex combination. - If
, is inside the triangle. - If one of
, is on an edge of . - If two of
, is at a vertex.
- If
Necessary Condition: If
is inside or on its sides, can be written as where . In these cases: inside implies . on edges or vertices implies .
Thus,
(c)
Given a triangle
determine if the point
is inside
To determine if
Barycentric coordinate equations
Point
This expands into:
From
Simplify both equations:
Reduce:
Solve the system by elimination: Subtract
Substitute
Thus:
The barycentric coordinates of
Since
Question-6
The following code is written to draw the outer surface of a cylinder as a quad-strip but nothing is seen on the screen. Assuming that lighting parameters and reflectance are properly set, explain why and suggest a remedy.
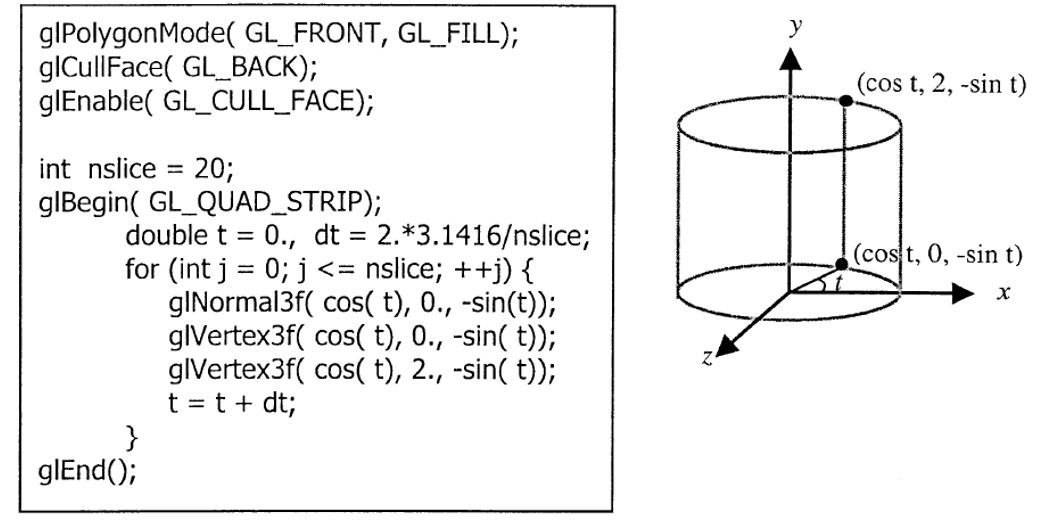
The issue is caused by incorrect vertex winding: the vertices are specified in clockwise order, making the quads back-facing by default. Since glCullFace(GL_BACK) is enabled, these polygons are culled, leaving nothing visible.
Remedy: Change the vertex order to counterclockwise for proper front-facing polygons:
glPolygonMode(GL_FRONT, GL_FILL);
glCullFace(GL_BACK);
glEnable(GL_CULL_FACE);
int nslice = 20;
glBegin(GL_QUAD_STRIP);
double t = 0., dt = 2. * 3.1416 / nslice;
for (int j = 0; j <= nslice; ++j) {
glNormal3f(cos(t), 0., -sin(t));
glVertex3f(cos(t), 2., -sin(t)); // Top vertex first
glVertex3f(cos(t), 0., -sin(t)); // Bottom vertex second
t += dt;
}
glEnd();Question-7
Consider the function sphere() that draws the outer surface of a unit sphere. Assume that a cylindrical map of the earth has been set up as the current texture and lighting is enabled. Suggest modifications on the function for supporting lighting calculation and the mapping of the texture on the sphere.
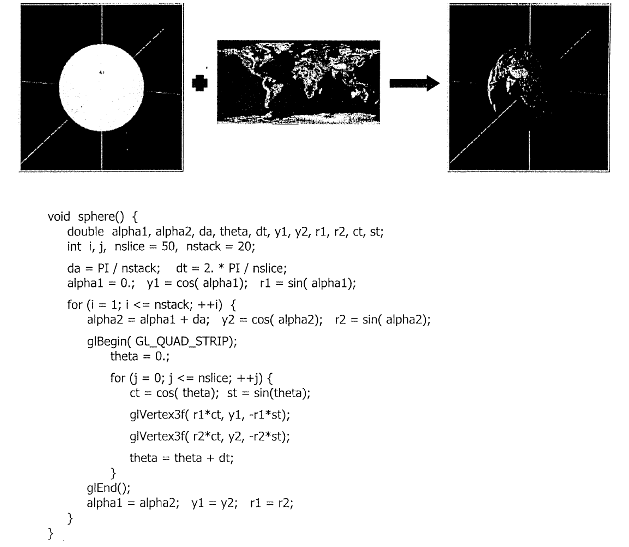
To modify the sphere() function for lighting and texture mapping:
Add Normals for Lighting: Use the vertex position as normals:
cglNormal3f(r1 * ct, y1, r1 * st); // For top vertex glNormal3f(r2 * ct, y2, r2 * st); // For bottom vertexImplement Texture Mapping: Calculate texture coordinates using spherical coordinates:
cglTexCoord2f(theta / (2.0 * M_PI), alpha1 / M_PI); // For top vertex glTexCoord2f(theta / (2.0 * M_PI), alpha2 / M_PI); // For bottom vertex
Updated sphere() Function:
void sphere() {
double alpha1, alpha2, da, theta, dtheta, y1, y2, r1, r2, ct, st;
int nslice = 50, nstack = 20;
da = M_PI / nstack;
dtheta = 2.0 * M_PI / nslice;
alpha1 = 0.0; y1 = cos(alpha1); r1 = sin(alpha1);
for (int i = 1; i <= nstack; ++i) {
alpha2 = alpha1 + da;
y2 = cos(alpha2); r2 = sin(alpha2);
glBegin(GL_QUAD_STRIP);
theta = 0.0;
for (int j = 0; j <= nslice; ++j) {
ct = cos(theta); st = sin(theta);
glTexCoord2f(theta / (2.0 * M_PI), alpha1 / M_PI);
glNormal3f(r1 * ct, y1, r1 * st); // Normal for top
glVertex3f(r1 * ct, y1, r1 * st);
glTexCoord2f(theta / (2.0 * M_PI), alpha2 / M_PI);
glNormal3f(r2 * ct, y2, r2 * st); // Normal for bottom
glVertex3f(r2 * ct, y2, r2 * st);
theta += dtheta;
}
glEnd();
alpha1 = alpha2; y1 = y2; r1 = r2;
}
}
