TOC-Regular language

Regular Language

+ Def: regular language

A language is regular if it is recognized by a DFA or an NFA.

To Prove a Language is regular, we need to construct a DFA or an NFA for the language.

Regular Operations

+ Def: Let $A$ and $B$ be languages.

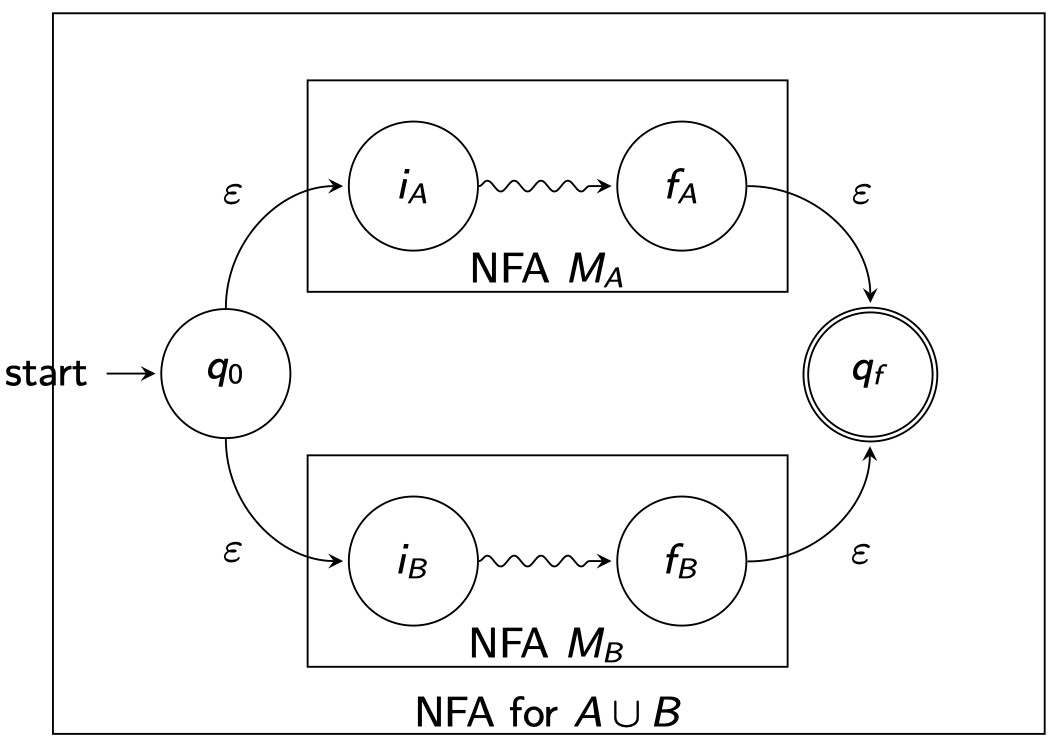
• Union : $A\cup B=x|x\in Aorx\in B$
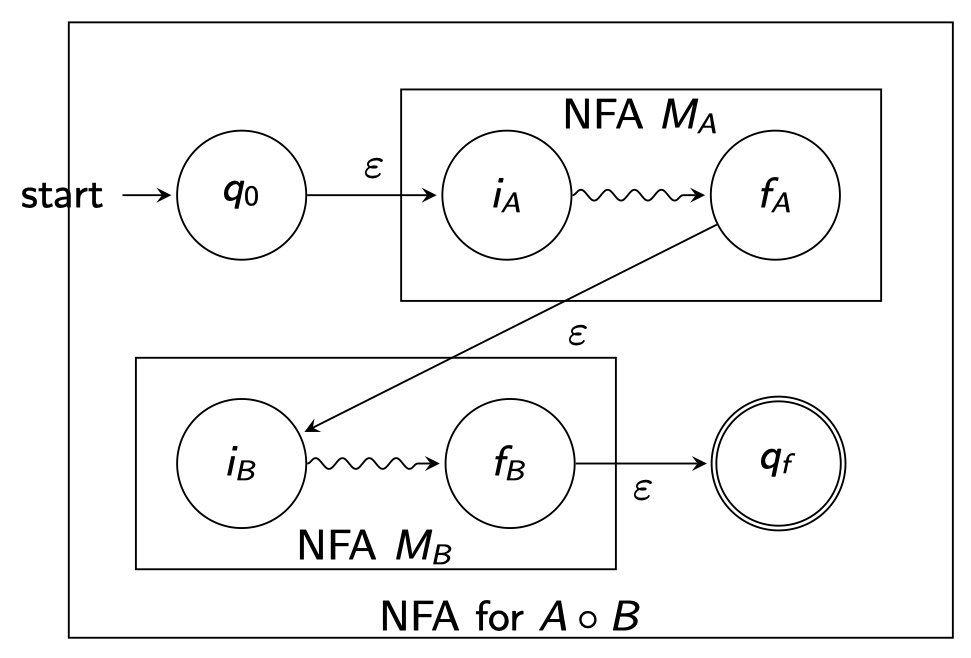
• Concatenation: $A\circ B=\{xy\mid x\in A\text{ and }y\in B\}$

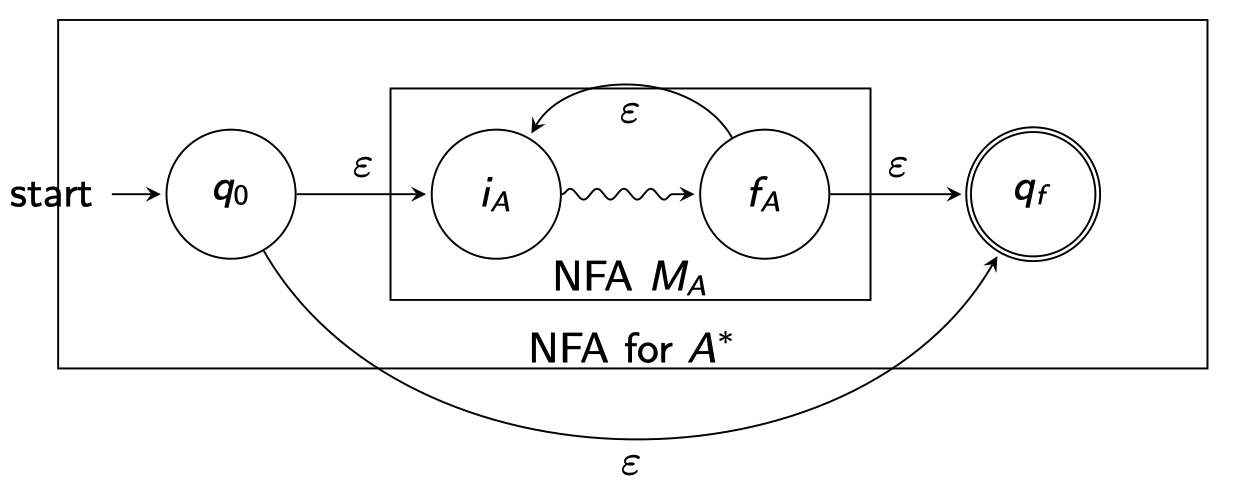
Star

$A^{\ast }=\{x_1{x}_2\dots x_k|k\ge 0andeach{x}_i\in A\}$

Note: each $x_i$ is a string in the language A. And $x_1{x}_2\dots x_k$ is the concatenation of $x_1,x_2$ , until $x_k$. Equivalently, $A^{\ast }=A_0\cup A_1\cup A_2\cup \dots$

+ Def: Star operator

Let $A$ be a language. $A^n$ for $n\in \mathbb{N}$ is recursively define

• $A^0=\{ϵ\}$
• $A^n=A^{n-1}\circ A$$$A^{*} = \cup_{i\in \mathbb{N}} A^{i}$$

Complement

Let $M=(Q,\mathrm{\Sigma },\delta ,q_0,F)$ be an arbitrary DFA. And we construct a new DFA $M^{\prime }=(Q,\mathrm{\Sigma },\delta ,q_0,Q\setminus F)$. Prove that $L(\bar{M})=L(M^{\prime })$.

Note:

• $Q\setminus F$ is the set difference.
• $L(\bar{M})={\mathrm{\Sigma }}^{\ast }\setminus L(M)$ is the set complement.

The goal $L(\bar{M})=L(M^{\prime })$ is understood as set equality.
Thus, we need to prove $\mathrm{\forall }w\in {\mathrm{\Sigma }}^{\ast }$, $w\in L(\bar{M})⟺w\in L(M^{\prime })$.

($\Rightarrow$)
Assume $w\in L(\bar{M})$.
Then $w\notin L(M)$.
Thus, DFA $M$ rejects $w$.
In other words, DFA $M$ halts on a non-final state $q_x$ by consuming all symbols in $w$.
By the construction of $M^{\prime }$, $q_x$ is a final state of $M^{\prime }$.
Thus, $M^{\prime }$ accepts $w$, and $w\in L(M^{\prime })$.

---

($\Leftarrow$)
Assume $w\in L(M^{\prime })$.
DFA $M^{\prime }$ accepts $w$.
In other words, DFA $M^{\prime }$ halts on a final state $q_y$ by consuming all symbols in $w$.
By the construction of $M^{\prime }$, $q_y$ is a non-final state of $M$.
Thus, $M$ rejects $w$, so $w\notin L(M)$.
Thus, $w\in L(\bar{M})$.

$L(\bar{M})=L(M^{\prime })$.

---

Let $\mathrm{\Sigma }=\{0,1\},\{A=\{00,1\}\},andB=\{10,1\}$.

• $A\cup B=\{00,1,10\}$
• $A\circ B=\{0010,001,110,11\}$
• $A^0=\{\epsilon \}$
• $A^1=\{00,1\}$
• $A^2=\{0000,001,100,11\}$
• $A^{\ast }=\{\epsilon ,00,1,0000,001,100,11,\dots \}$

Closure

+ Theorem (Closure)

Regular language is closed under union, concatenation, star and complement.

if A and B are two regular languages, then $A\cup B$, $A\circ B$, and $A^{\ast }$ are also regular languages.

Construct an NFA for $A\cup B$.

Construct an NFA for $A\circ B$.

Construct an NFA for $A^{\ast }$.

Regular Expression

Regular languages can be recursively constructed. A regular expression describes the common pattern the strings in a regular language (machine independent).

+ Def: Regular expression (Recursive Definition)

$R$ is a regular expression over $\mathrm{\Sigma }$ if $R$ is $(BaseCase)$

• $a$ for some $a\in \mathrm{\Sigma }$,
• $ϵ$, or
• $\mathrm{\varnothing }$

$(Recursion)$

• $(R_1\cup R_2)$, where $R_1$ and $R_2$ are regular expressions,
• $R_1\circ R_2$, where $R_1$ and $R_2$ are regular expressions, or
• $R_1^{\ast }$, where $R_1$ is a regular expression.

Languages Defined by Regular Expression

+ Def: Let $R$ be a regular expression. The language $L(R)$ defined by $R$ is

$Basecase:$

• $L(\mathrm{\varnothing })=\mathrm{\varnothing }$,
• $L(ϵ)=\{ϵ\}$,
• $\mathrm{\forall }a\in \mathrm{\Sigma }$, $L(a)=\{a\}$.

$Recursion:$

• if $R=R_1\cup R_2$, then $L(R)=L(R_1)\cup L(R_2)$
• if $R=R_1\circ R_2$, then $L(R)=L(R_1)\circ L(R_2)$
• if $R=R_1^{\ast }$, then $L(R)=L(R_1{)}^{\ast }$

Example:

Suppose $\mathrm{\Sigma }=\{0,1\}$. Describe the language defined by the following regular expressions in English.

• $0^{\ast }{10}^{\ast }$
• ${\mathrm{\Sigma }}^{\ast }1{\mathrm{\Sigma }}^{\ast }$
• $(0\cup ϵ)(1\cup ϵ)$
• $(\mathrm{\Sigma }\mathrm{\Sigma }{)}^{\ast }$
• ${\mathrm{\Sigma }}^{\ast }\mathrm{\varnothing }$ Match nothing

Equivalence of Regular Expression and Finite Automata

+ Theorem

Regular expressions are equivalent to finite automata.

The proof has two steps.

1. The language defined by a regular expression can be recognized by a finite automaton.
2. The conversion is also doable vice versa.

The conversion from a regular expression to an NFA is trivially ensured by the closure property . So, we only need to convert NFA to regular expressions.

Conversion from NFA to Regular Expression

The Conversion requires generalized NFA, which is a special type of NFA.

Only one start state and one final state. The start state is different from the final state. The transition function is

• $\delta :(Q\setminus \{q_f\})\times (Q\setminus \{q_0\})\to R$

Suppose $\delta (a,b)\to R$

• It means transition from $a$ to $b$ requires $R$.
• If the GNFA has only 2 states $q_0$ and $q_f$, then the label on the transition is the regular expression for the language.
• Thus, the conversion recursively merges states and transitions of the generalized NFA.

\begin{algorithm}
\caption{Convert NFA$_\varepsilon$ to 2-state gNFA}
\begin{algorithmic}
\Input An NFA $N = (Q, \Sigma, \delta, q_0, F)$
\Output A regular expression which defines $L(N)$
\STATE $N' \gets N$ // convert the domain and codomain of the transition function
\STATE $Q' \gets Q' \cup \{q_0', q_f'\}$
\STATE $\delta'(q_0', q_0) = \varepsilon$
\FORALL{$q \in F$}
    \STATE $\delta'(q, q_f') = \varepsilon$
\ENDFOR
\FORALL{state $q$ in $Q'$ except $q_0'$ and $q_f'$}
    \STATE $Q' \gets Q' \setminus \{q\}$
    \FORALL{state $q_i$ in $Q'$ except $q_f'$}
        \FORALL{state $q_j$ in $Q'$ except $q_0'$}
            \STATE \textbf{Suppose} $\delta'(q_i, q) = R_1$, $\delta'(q, q) = R_2$, $\delta'(q, q_j) = R_3$, and $\delta'(q_i, q_j) = R_4$
            \STATE $\delta'(q_i, q_j) = ((R_1)(R_2)^* R_3) \cup (R_4)$
        \ENDFOR
    \ENDFOR
\ENDFOR
\RETURN $\delta'(q_0', q_f')$
\end{algorithmic}
\end{algorithm}