Network Deconvolution

Network deconvolution as a general method to distinguish direct dependencies in networks

---

Network Deconvolution

Removes the combined effect of all indirect paths of arbitrary length in a closed-form solution

By exploiting eigen-decomposition and infinite-series sums

---

Assumptions

$g_{i,j}^{obs}$ represents the similarity value between the observed patterns of variables $i$ and $j$ in the network.

定义一个观测到的相似度矩阵，矩阵里的值可以是变量$i,j$的关系，也可以是其他的相似度值

---

Assumptions

We assume that the observed dependency matrix, $G_{obs}$, comprises both direct and indirect dependency effects

$$G_{obs}=G_{dir}+G_{indir}$$

观测矩阵包含直接和间接依赖效应

---

Assumptions

Indirect contributions

• Can be length 2 or higher
• Can be multiple effects along varying paths
• Not included Self-loops

间接影响可以是长度为2或更长的边,不包括自环

$$G_{indir}=G_{idr}^2+G_{dir}^3+...$$

The power associated with each term in $G_{indir}$ corresponds to the level of indirection contributed by that term. 幂次指的是间接程度

---

Derivation

$$G_{obs}=G_{dir}+G_{indir}$$

By using the eigen decomposition principle, we have

$$G_{dir}=U{\mathrm{\Sigma }}_{dir}{U}^{-1}$$

---

Derivation

$$\begin{array}{rl}{G}_{dir}+G_{indir}\stackrel{(a)}{=}& G_{dir}+G_{dir}^2+\cdots \\ \stackrel{(b)}{=}& \left(U{\mathrm{\Sigma }}_{dir}{U}^{-1}\right)+\left(U{\mathrm{\Sigma }}_{dir}^2{U}^{-1}\right)+\cdots \\ =& U({\mathrm{\Sigma }}_{dir}+{\mathrm{\Sigma }}_{dir}^2+\cdots )U^{-1}\\ =& U\left(\begin{array}{cccc}\sum _{i\ge 1}({\lambda }_1^{dir}{)}^i& 0& \cdots & 0\\ 0& \ddots & & ⋮\\ ⋮& & \ddots & 0\\ 0& \cdots & 0& \sum _{i\ge 1}({\lambda }_n^{dir}{)}^i\end{array}\right)U^{-1}\end{array}$$

---

Derivation

$$\sum _{j\ge 1}^{+\mathrm{\infty }}({\lambda }_i^{dir}{)}^j={\lambda }_i^{dir}+{\lambda }_i^{2dir}+{\lambda }_i^{3dir}+\cdots =\frac{{\lambda }_i^{dir}}{1-{\lambda }_i^{dir}}$$$$\begin{array}{r}{G}_{dir}+G_{indir}\stackrel{(c)}{=}U\left(\begin{array}{cccc}\frac{{\lambda }_1^{dir}}{1-{\lambda }_1^{dir}}& 0& \cdots & 0\\ 0& \ddots & & ⋮\\ ⋮& & \ddots & 0\\ 0& \cdots & 0& \frac{{\lambda }_n^{dir}}{1-{\lambda }_n^{dir}}\end{array}\right)U^{-1}.\end{array}$$

---

Derivation

By using the eigen decomposition of the observed network $G_{obs}$, we have $G_{obs}=U{\mathrm{\Sigma }}_{obs}{U}^{-1}$, where

$${\mathrm{\Sigma }}_{obs}=\left(\begin{array}{ccc}{\lambda }_1^{obs}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\lambda }_n^{obs}\end{array}\right)$$$$\frac{{\lambda }_i^{dir}}{1-{\lambda }_i^{dir}}={\lambda }_i^{obs}\mathrm{\forall }1\le i\le n$$$${\lambda }_i^{dir}=\frac{{\lambda }_i^{obs}}{{\lambda }_i^{obs}+1}\mathrm{\forall }1\le i\le n$$$$G_{dir}=U{\mathrm{\Sigma }}_{dir}{U}^{-1}$$

---

Network deconvolution Methods

1. Linear Scaling Step

2. Decomposition Step

3. Deconvolution Step

---

Linear Scaling Step

The observed dependency matrix is scaled linearly so that all eigenvalues of the direct dependency matrix are between −1 and 1.

线性缩放使所有特征值在 -1～1 之间

---

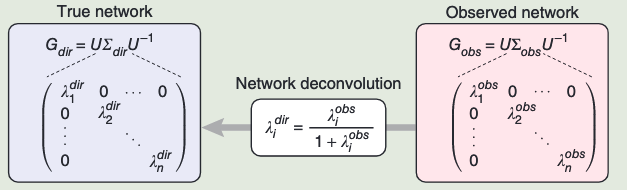
Decomposition Step

The observed dependency matrix Gobs is decomposed to its eigenvalues and eigenvectors such that

$$G_{\text{obs}}=U{\mathrm{\Sigma }}_{\text{obs}}{U}^{-1}$$

Where:

• $U$ is the matrix of eigenvectors,
• ${\mathrm{\Sigma }}_{\text{obs}}$ is a diagonal matrix containing the eigenvalues of $G_{\text{obs}}$,
• $U^{-1}$ is the inverse of the eigenvector matrix $U$.

将观察到的依赖矩阵分解为特征值和特征向量

---

Deconvolution Step

A diagonal eigenvalue matrix $\mathrm{\Sigma }dir$ is formed whose $i-th$ component is

$${\lambda }_i^{\text{dir}}=\frac{{\lambda }_i^{\text{obs}}}{{\lambda }_i^{\text{obs}}+1}$$

Then, the output direct dependency matrix $G_{\text{dir}}$ is obtained as

$$G_{dir}=U{\mathrm{\Sigma }}_{dir}{U}^{-1}$$

---

Several network applications:

• Distinguishing direct targets in gene expression regulatory networks
  • 区分基因表达调控网络中的直接目标
• Recognizing directly interacting amino-acid residues for protein structure prediction from sequence alignments
  • 通过序列比对识别直接相互作用的氨基酸残基以预测蛋白质结构
• Distinguishing strong collaborations in co-authorship social networks using connectivity information alone.
  • 仅使用连接信息来区分共同创作社交网络中的强协作。

---

Thanks for your attention