AllenYGY's Blog

Appearance

递归 ​

什么是递归? ​

程序调用自身的编程技巧称为递归 Recursion

  • 递归作为一种算法在程序设计语言中广泛应用。
  • 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。
  • 递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。
  • 一般来说，递归需要有边界条件、递归前进段和递归返回段。
  • 当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

递归的能力在于用有限的语句来定义对象的无限集合。

递归 VS 循环 ​

递归：你打开面前这扇门，看到屋里面还有一扇门。你走过去，发现手中的钥匙还可以打开它，你推开门，发现里面还有一扇门，你继续打开它。若干次之后，你打开面前的门后，发现只有一间屋子，没有门了。然后，你开始原路返回，每走回一间屋子，你数一次，走到入口的时候，你可以回答出你到底用这你把钥匙打开了几扇门。

循环：你打开面前这扇门，看到屋里面还有一扇门。你走过去，发现手中的钥匙还可以打开它，你推开门，发现里面还有一扇门（若前面两扇门都一样，那么这扇门和前两扇门也一样；如果第二扇门比第一扇门小，那么这扇门也比第二扇门小，你继续打开这扇门，一直这样继续下去直到打开所有的门。但是，入口处的人始终等不到你回去告诉他答案。

递归三要素 ​

1. 明确递归终止条件（递归出口）

我们知道，递归就是有去有回，既然这样，那么必然应该有一个明确的临界点，程序一旦到达了这个临界点，就不用继续往下递去而是开始实实在在的归来。换句话说，该临界点就是一种简单情境，可以防止无限递归。

2. 给出递归终止时的处理办法

我们刚刚说到，在递归的临界点存在一种简单情境，在这种简单情境下，我们应该直接给出问题的解决方案。一般地，在这种情境下，问题的解决方案是直观的、容易的。

3. 提取重复的逻辑，缩小问题规模

我们在阐述递归思想内涵时谈到，递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决。从程序实现的角度而言，我们需要抽象出一个干净利落的重复的逻辑，以便使用相同的方式解决子问题。

实战训练 ​

参赛成绩 ​

题目描述 ​

柳州传说是歌仙刘三姐的传歌之地，最近举办了一次山歌大赛。 在这个项目中，参赛者每次完成一个段都会得到一个分数。总分数的计算方式基于一个特殊 的数学表达式 f(x,n)。表达式 f(x,n) 的定义如下：

4e4fe6b7f35886e021f9a1fa1334df4.jpg

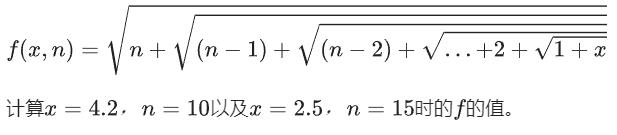
其中，x 表示参赛者的基本得分，n 表示参赛者完成的山歌段落数。

津津、菲菲和皮皮的任务是编写一个程序，并计算选手 A（x=4.2,n=10）、选手 B（x=2.5,n=15） 时 f(x,n)的值

输入格式 ​

输入x和n。

输出格式 ​

函数值，保留两位小数。

样例 ​

Input

txt
4.2 10

Output

txt
3.68

CODE ​

cpp
#include<bits/stdc++.h>
#include<iostream>
#define int long long
#define endl '\n'
using namespace std;

double f(double x, int n){
    if(n==1) return sqrt(1+x);
    return sqrt(n+f(x,n-1));
}

signed main() {
    double x; 
    int n;
    cin>>x>>n;
    cout<<fixed<<setprecision(2)<<f(x,n)<<endl;
    return 0;
}

Hermite多项式 ​

题目描述 ​

用递归的方法求 Hermite 多项式的值。

hn(x)={1if n=02xif n=12xhn−1(x)−2(n−1)hn−2(x)if n>1

输入格式 ​

给定的 x 和正整数 n

输出格式 ​

对给定的 x 和正整数 n，求多项式的值。

样例 ​

Input

txt
1 2

Output

txt
4.00

CODE ​

cpp
#include<bits/stdc++.h>
#include<iostream>
#define int long long
#define endl '\n'
using namespace std;

double h(double x, int n){
    if(n==0) return 1;
    if(n==1) return 2*x;
    return 2*x*h(x,n-1)-2*(n-1)*h(x,n-2);
}

signed main() {
    int n;
    double x;
    cin>>n>>x;
    cout<<fixed<<setprecision(2)<<h(x,n)<<endl;
    return 0;
}

奶牛的故事 ​

题目描述 ​

有一头母牛，从第二年起，它每年年初生一头小母牛。每头小母牛从第四个年头开始，每年年初也生一头小母牛。请编程实现在第n年的时候，共有多少头母牛？

输入格式 ​

输入数据由多个测试实例组成，每个测试实例占一行，包括一个整数n(0<n<55)，n的含义如题目中描述。

n=0表示输入数据的结束，不做处理。

输出格式 ​

对于每个测试实例，输出在第n年的时候母牛的数量。每个输出占一行。

样例 ​

Input

2
4
5
0

Output

2
4
6

题解 ​

第n年的牛的数量为：n-1年的数量和今年新出生的牛的数量 今年新出生的牛的数量为 n-3 年前牛的数量

CODE ​

cpp
#include <bits/stdc++.h>
#include <iostream>
#define int long long
#define endl '\n'
using namespace std;

const int MOD = 1000;
const int MAXN = 1000000;

int val[MAXN] = {0};

void solve(int x)
{

    if(val[x]!=0){
        cout << val[x] << endl;
        return;
    }
    val[1]=1;
    val[2]=2;
    val[3]=3;
    for(int i=4;i<=x;i++){
        val[i]=(val[i-1]+val[i-3]);
    }
    cout << val[x] << endl;
}

signed main()
{
    int x;
    cin >> x;
    while (x)
    {
        solve(x);
        cin >> x;
    }
    return 0;
}