DSA-AS-1

Problem I

\begin{algorithm}
\caption{GETminimum(A)}
\begin{algorithmic}
\State \textbf{SORT}(A)
\If{$A[0] - A[A.\text{length} - 1] < 0$}
    \State \Return $A[0] - A[A.\text{length} - 1]$
\Else
    \State $min \gets \infty$
    \For{$i \gets 1$ \textbf{to} $A.\text{length} - 1$}
        \If{$A[i] - A[i - 1] < min$}
            \State $min \gets A[i] - A[i - 1]$
        \EndIf
    \EndFor
\EndIf
\State \Return $min$
\end{algorithmic}
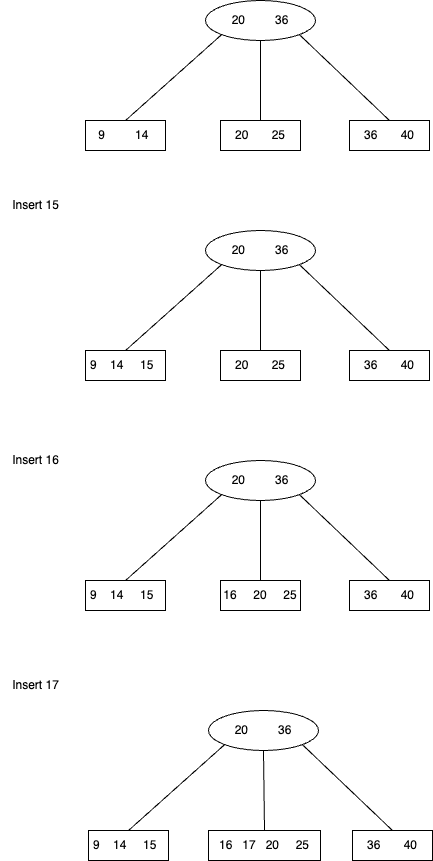
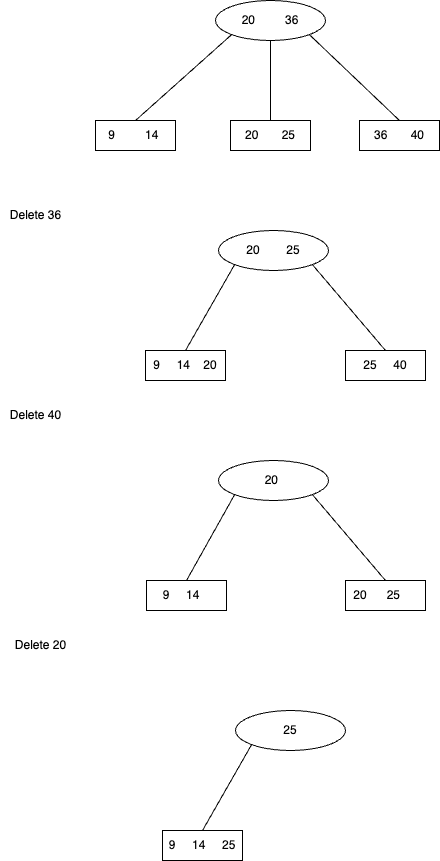
\end{algorithm}

Problem II

1. 
2. 
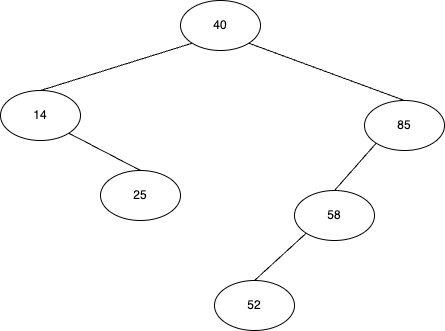
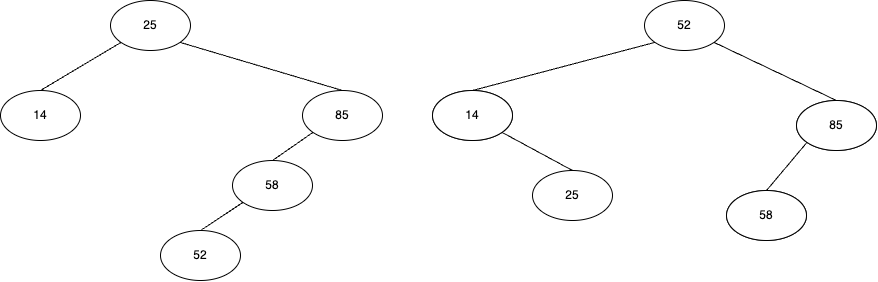
3. |14|25|40|52|58|85|

Problem III

3.1

a. Initial State

              52|2              
        ┌───────┴───────┐       
      15|1            85|0      
    ┌───┴───┐                   
   8|0    31|0

Insert 82:

              52|2              
        ┌───────┴───────┐       
      15|1            85|1      
    ┌───┴───┐       ┌───┘       
   8|0    31|0    82|0

Insert 6:

                              52|3                              
                ┌───────────────┴───────────────┐               
              15|2                            85|1              
        ┌───────┴───────┐               ┌───────┘               
       8|1            31|0            82|0                      
    ┌───┘                                                       
   6|0

Insert 65:

                              52|3                              
                ┌───────────────┴───────────────┐               
              15|2                            82|1              
        ┌───────┴───────┐               ┌───────┴───────┐       
       8|1            31|0            65|0            85|0      
    ┌───┘                                                       
   6|0

b.

1

                              52|3                              
                ┌───────────────┴───────────────┐               
               8|1                            82|2              
        ┌───────┴───────┐               ┌───────┴───────┐       
       6|0            15|0            65|1            85|1      
                                        └───┐           └───┐   
                                          72|0            95|0

2

                              65|3                              
                ┌───────────────┴───────────────┐               
              15|2                            82|2              
        ┌───────┴───────┐               ┌───────┴───────┐       
       8|1            31|0            72|0            85|1      
    ┌───┘                                               └───┐   
   6|0                                                    95|0

3

                              52|3                              
                ┌───────────────┴───────────────┐               
              15|2                            85|2              
        ┌───────┴───────┐               ┌───────┴───────┐       
       8|1            31|0            65|1            95|0      
    ┌───┘                               └───┐                   
   6|0                                    72|0

3.2

1. Insertion Time: To insert an element into an [[AVL]] tree, we perform a binary search to find the correct position for the new element and then possibly perform some rotations to maintain the [[AVL]] property. The time complexity of both these operations is $O(logn)$ because the tree is balanced.

2. Building the Tree: If we insert $n$ distinct integers into an [[AVL|AVL]] tree, each insert operation takes $O(logn)$ time. Since there are $n$ elements, the total time to build the tree is $O(nlogn)$.

3. In-order Traversal: Once the [[AVL]] tree is built, we can perform an in-order traversal to retrieve the elements in sorted order. An in-order traversal of a binary search tree visits the nodes in ascending order, which is what we want for sorting. The time complexity for in-order traversal is $O(n)$, as each node is visited exactly once.

4. Total Time Complexity: The total time complexity of sorting an array using an [[AVL|AVL]] tree is the time to build the tree ($O(nlogn)$) plus the time for the in-order traversal ($O(n)$). Hence, the overall time complexity is $O(nlogn)$.

Therefore, we have shown that using an [[|AVL]] tree to sort an array of distinct integers has a time complexity of $O(nlogn)$.

Problem IV

a.

$(L=\lfloor \frac{\text{Size of one block}}{\text{Size of each employee record}}\rfloor =\lfloor \frac{2048}{128}\rfloor =16)$

$(M=\lfloor \frac{\text{Size of one block}}{\text{Size of a primary key + Size of a pointer}}\rfloor +1)$

$(M=\lfloor \frac{2048}{8+4}\rfloor +1=\lfloor \frac{2048}{12}\rfloor +1=170+1=171)$

• $L=16$: Each leaf node can hold up to 16 records.
• $M=171$: Each internal node can have up to 171 children (170 keys + 1 extra pointer).

b.

1. 
2.