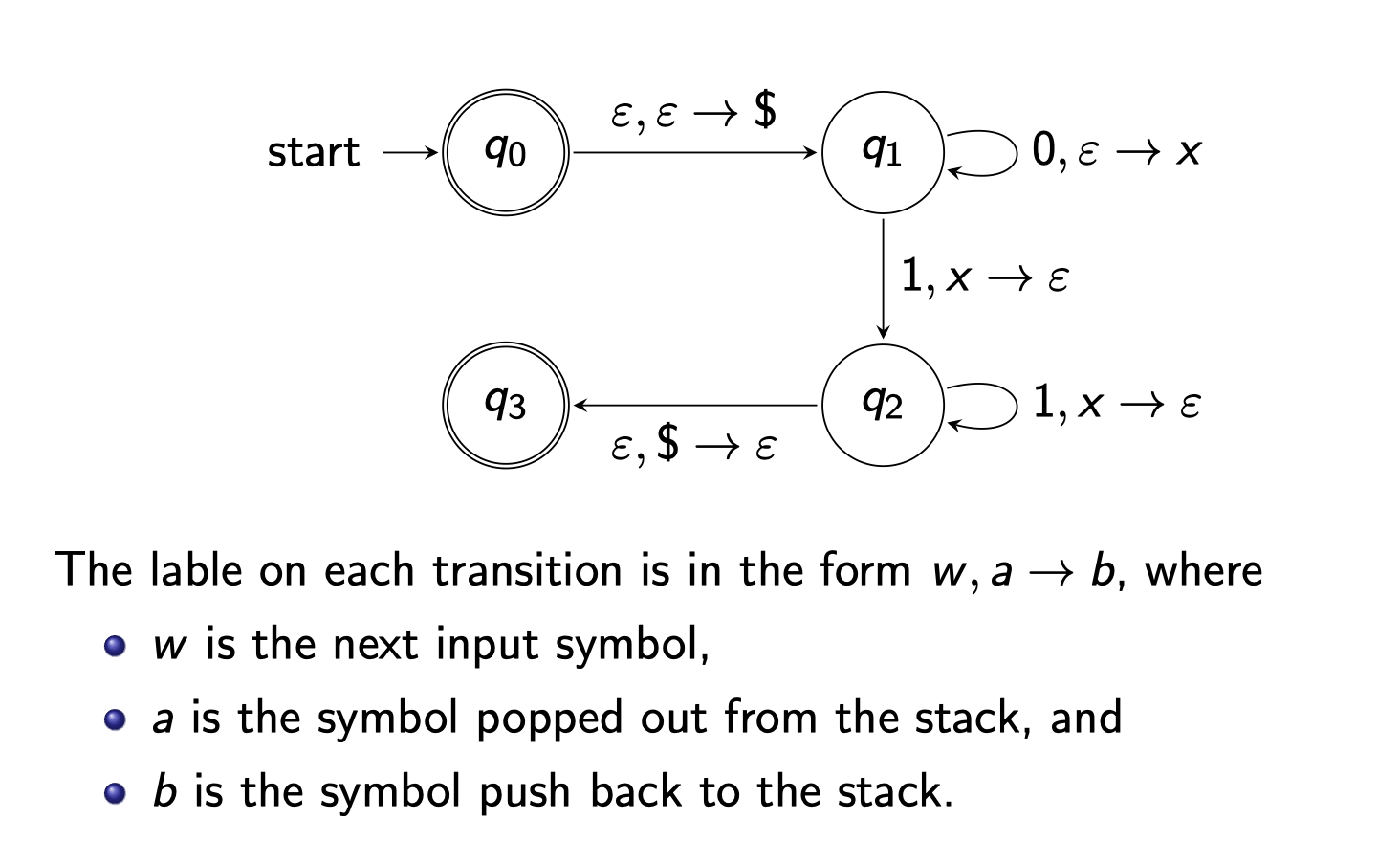
TOC-PDA

To access the infinite memory space, an NFA is upgraded by a stack. A stack has these basic operations.

• Push
• Pop

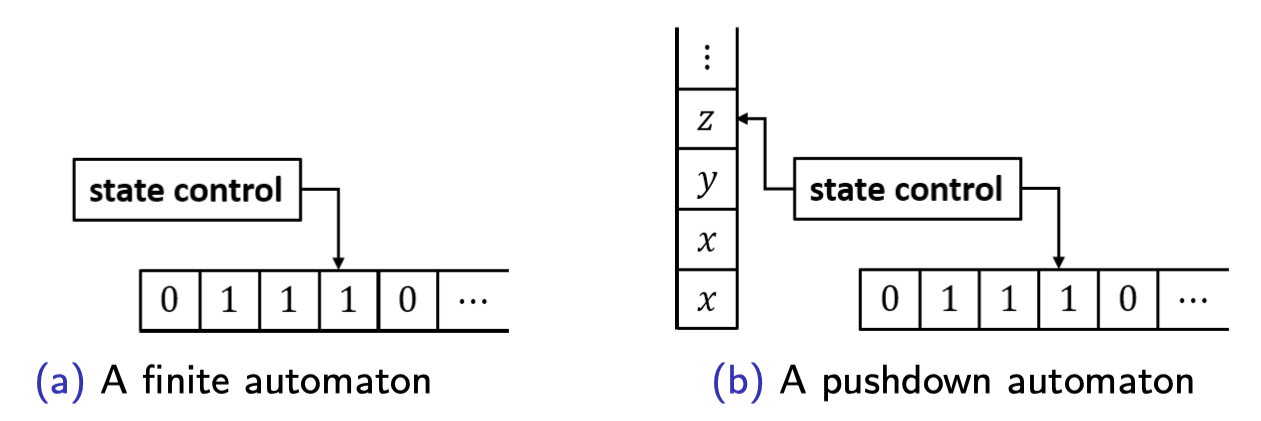
The computational model combines a finite state machine and a stack is called pushdown automata $(PDA)$.

PDA

A pushdown automaton is a 6-tuple $(Q,\mathrm{\Sigma },\mathrm{\Gamma },\delta ,q_0,F)$, where

• $Q$ is the finite set of states;
• $\mathrm{\Sigma }$ is the finite input alphabet;
• $\mathrm{\Gamma }$ is the finite stack alphabet;
• $\delta :Q\times {\mathrm{\Sigma }}_{ϵ}\times {\mathrm{\Gamma }}_{ϵ}\to P(Q\times {\mathrm{\Gamma }}_{ϵ})$ is the transition function;
• $q_0\in Q$ is the initial state;
• $F\subseteq Q$ is the set of final states;

The transition function $\delta :Q\times {\mathrm{\Sigma }}_{ϵ}\times {\mathrm{\Gamma }}_{ϵ}\to P(Q\times {\mathrm{\Gamma }}_{ϵ})$ is understood as

Transition Function

If:

• The current state is $q\in Q$
• The next input symbol is $s\in {\mathrm{\Sigma }}_{ϵ}$
• The symbol on top of the stack is $r\in {\mathrm{\Gamma }}_{ϵ}$

Then:

• The next state is $q^{\prime }\in Q$
• The new stack symbol on the top is $r^{\prime }\in {\mathrm{\Gamma }}_{ϵ}$

PDA is defined from NFA.

• $ϵ$ is included in ${\mathrm{\Sigma }}_{ϵ}$ and ${\mathrm{\Gamma }}_{ϵ}$.
• The domain of $\delta$ is the power set $P(Q\times {\mathrm{\Gamma }}_{ϵ})$.
• $PDA$ has multiple choices for the next state.

Computation on PDA

An input string $w=w_1{w}_2\cdots w_n$ is accepted by a PDA $M$ if there exists a sequence of states $t_0,t_1,\cdots ,t_n\in Q$ and a sequence of strings $r_0,r_1,\cdots ,r_n\in {\mathrm{\Gamma }}^{\ast }$ such that:

1. $t_0=q_0$ (where $t_0$ is the initial state);
2. $r_0=\epsilon$ (the stack is empty initially);
3. $t_n\in F$ ($t_n$ is a final state); and
4. For $i=0,\cdots ,n$,$$(t_{i+1},b)\in \delta (t_i,w_{i+1},a),$$where $r_i=sa$ and $r_{i+1}=sb$ for some $a,b\in {\mathrm{\Gamma }}_{\epsilon }$ and $s\in {\mathrm{\Gamma }}^{\ast }$.

The last condition explains a transition.

• Each string $r_i$ is the content of the stack.
• The leftmost symbol in $r_i$ is at the bottom of the stack.
• The rightmost symbol in $r_i$ is at the top of the stack ($a$ and $b$).
• The PDA consumes $w_{i+1}$, changes the stack symbol from $a$ to $b$, and shifts to state $t_{i+1}$.

Example

A PDA for $0^n{1}^n$