Bioinfo Matrix Operations

---

Matrix Factorization

Non-negative dataset

• Counters: 计数
• Quantities: 数量数据
• Intensities: 强度数据

NMF

NMF is used in a compositional model. Data are assumed to be non-negative

Every data vector is explained as a purely constructive linear composition of a set of bases

• $V=\sum _i{w}_i{B}_i$
• The bases $B_i$ are in the same domain as the data

Constructive composition: no subtraction allowed

• Weights $w_i$ must be non-negative
• All components of bases $B_i$ must be non-negative

Data Does Not Need to Be Non-Negative:

• Unlike traditional NMF where data is assumed to be non-negative, this generalization allows data to exist in any quadrant, including negative regions.

Non-Negativity Constraint:

• Only the weights must remain non-negative, regardless of the data’s distribution.

• The model preserves the fundamental principle of constructive addition without subtracting components.

Minimizing Divergence

• $L_2$ Divergence: $D(V,BW)=\sum _i\sum _j(V_{ij}-B{W}_{ij}{)}^2$
• $KL$ Divergence: $\sum _i\sum _j(V_{ij}log\frac{V_{ij}}{B{W}_{ij}}+V_{ij}-B{W}_{ij})$

Iterative solution:

• $B=[VPinv(W{)}_{+}]$
• $W=[Pinv(B)V{]}_{+}$
• Subscript $+$ indicates thresholding -values to 0.表示对负值进行阈值处理，将所有负值设置为 0，确保非负性。

NMF is not unique

NMF is not hierarchical （非负矩阵分解并非分层结构）

1. Rank-1 NMF

• Rank-1 分解：将数据矩阵分解为单一基向量和权重向量的乘积。

• 左侧的原始矩阵被近似分解为右侧的基矩阵和权重矩阵。

• 这种低秩分解可以很好地捕捉数据的主成分，但可能忽略细节。

2. Rank-2 NMF

• Rank-2 分解：将数据矩阵分解为两个基向量和对应权重的组合。

• 分解为两个矩阵之和：

• 数据矩阵通过两个基成分加权求和表示。

• Rank-2 分解能够捕捉更多的结构信息，但分解结果与 Rank-1 不具有分层关系。

非分层结构：

• 增加秩 并不会简单地在前一级结果的基础上扩展，而是需要重新计算分解。

秩的选择影响分解的质量、稀疏性和可解释性。

• 稀疏性（Sparsity）：较低秩分解更稀疏，较高秩分解捕捉更多细节。
• 可解释性（Interpretability）：秩的选择会影响基向量的可解释性。
• 统计保真度（Statistical Fidelity）：较高秩通常能够更好地重构数据，但可能过拟合。
• 最佳秩  k  的选择： 并无统一的理论方法，需要通过实验来确定最优秩。

NMF General framework

Gradient descent generally slow

Stochastic gradient descent inappropriate

Key Approach: Alternating Minimization

1. Pick starting point L₀ and R₀
2. while not converged do
   3. Keep R fixed, optimize L
   4. Keep L fixed, optimize R
   5. end while

Update steps 3 and 4 are easier than solving the full problem.

This approach is also called alternating projections or (block) coordinate descent.

Starting Point Options

• Random
• Multi-start initialization: Try multiple random starting points, run a few epochs, continue with the best.
• Based on SVD
• ...

NMF in Bioinformatics

Example - 1

非负矩阵分解（NMF） 来识别癌症基因组数据中的多维模块，通过综合分析多平台基因组数据实现： link

• DNA 甲基化（DM）
• miRNA 表达（ME）
• 基因表达（GE）

The Joint NMF Framework for Integrative Analysis

Example - 2

本示例展示了如何使用 种子非负矩阵分解（Seeded NMF） 来解析空间转录组学（Spatial Transcriptomics, ST）数据。

• 空间转录组学（ST）技术：
  • 生成基因表达图谱，同时保留组织的空间上下文。
  • 每个空间点（spots）通常捕获多个细胞，缺乏单细胞分辨率。
• 目标：
  • 通过集成单细胞 RNA 测序（scRNA-seq）数据和 ST 数据，使用 NMF 进行去卷积（Deconvolution）。
  • 解释每个空间点的细胞组成。

SPOTlight

SPOTlight 使用种子 NMF 回归（Seeded NMF Regression） 来实现目标：

1. 学习单细胞数据中的主题特征（signatures）：

   • 使用单细胞 RNA 测序数据，识别不同细胞类型的基因表达特征。

2. 解析空间数据：

   • 将这些特征应用于 ST 数据，找到每个空间点的最佳加权细胞类型组合。

NMF 分解过程

• 初始化 (NMF Initialization)

• 数据分解为： $V\approx W\times H$

  • W（基矩阵）：基因 × 主题（gene × topic）。
  • H（系数矩阵）：主题 × 细胞（topic × cell）。
  • V：基因 × 细胞的原始表达数据矩阵。

• 分解步骤 (Factorization)

• 将 ST 数据 V′V' 分解为基矩阵 WW 和系数矩阵 HH：

  • WW：基因 × 主题矩阵（与单细胞特征关联）。
  • HH：主题 × 空间点的权重矩阵。

解析结果：Spot 去卷积

• NNLS（非负最小二乘法）：
  • 用于优化权重矩阵 HH，以解释每个空间点的细胞组成。
• 结果展示：
  • 每个空间点（Spot 1、Spot 2 等）分解为多个细胞类型的加权组合，显示在饼图中。
  • 例如：
    • Spot 1: 17% 细胞类型 A，17% 细胞类型 B，33% 细胞类型 C 等。

1. 种子 NMF 的优势：
   • 使用单细胞数据作为“种子”初始化 WW，提高结果的生物学可解释性。
2. 空间数据去卷积：
   • SPOTlight 将单细胞数据与空间数据结合，揭示每个空间点的细胞组成。
3. 应用场景：
   • 理解组织中的空间细胞异质性，特别在癌症等研究中具有重要意义。

• Paper
• SPOTlight Code

总结：通过种子 NMF 回归方法，SPOTlight 有效解析空间转录组学数据，结合单细胞数据揭示组织的细胞组成。

Example - 3

Paper

背景：人类癌症中的突变特征

目标：通过非负矩阵分解（NMF）方法，揭示不同癌症样本中的突变特征（mutational signatures）。 数据：

• 横轴：癌症样本（不同的癌症类型）。
• 纵轴：突变特征（SBS1、SBS2、SBS3 等）。
• 点的大小与颜色：代表不同特征在特定癌症样本中的突变贡献程度。

主要内容解析

1. 横轴（Cancer Samples）：
   • 不同的癌症类型（如乳腺癌、肺癌等）。
   • 每一列表示一个癌症样本集合。
2. 纵轴（Mutation Signatures）：
   • SBS（Single Base Substitution）特征：代表单碱基替换的不同突变模式（SBS1、SBS2 等）。
   • 每一行代表一种特定的突变特征。
3. 点的表示：
   • 颜色：不同颜色表示特征的突变机制，例如：
     • 橙色：APOBEC 活性
     • 紫色：DNA 修复缺陷
     • 蓝色：化学暴露或辐射
   • 点的大小：表示特定突变特征在癌症样本中的贡献比例。
   • 颜色深浅：表明突变数量的多少，越深表示突变数量越高。
4. 右侧图例（Proposed Aetiology）：
   • 列出了每个突变特征背后的潜在机制，例如：
     • SBS1：5-甲基胞嘧啶脱氨
     • SBS3：BRCA1/2 突变导致的 DNA 修复缺陷
     • SBS4：与烟草吸烟相关

NMF 的应用

• 非负矩阵分解（NMF）：
  • 将突变数据矩阵分解为：$X\approx W\times H$
    • X：突变数据矩阵（癌症样本 × 突变特征）。
    • W：基因组突变的特征矩阵（表示不同特征的突变机制）。
    • H：样本中的权重矩阵（表示各特征在不同样本中的贡献）。
  • NMF 的作用：
    • 提取癌症样本中的突变特征。
    • 识别不同癌症类型中的主要突变机制。

关键结果

1. 突变特征（SBS）与癌症类型的关联：

   • 某些突变特征（如 SBS3）与DNA 修复缺陷相关（例如 BRCA1/2 突变）。
   • SBS4 明显与烟草吸烟相关。
   • 特定癌症类型的突变模式与特定环境因素或基因缺陷有关。

2. 数据可视化：

   • 点图展示了不同癌症样本中各突变特征的贡献大小。
   • 可直观地识别出哪些突变机制在某些癌症类型中占主导地位。

3. 突变机制：

   • 提供了癌症突变的潜在生物学机制（如化学暴露、DNA 修复缺陷等），对癌症的病因研究具有重要意义。

总结

通过 NMF 分解：

1. 揭示了人类癌症中的突变特征及其贡献程度。
2. 帮助识别不同癌症类型中的主要突变机制（例如化学暴露、DNA 修复缺陷等）。
3. 为癌症研究提供了一个整合、系统化的框架，揭示突变数据中的潜在模式和生物学机制。

Matrix Imputation

• Proteomics
• Single cell RNA-seq
• Spatial Transcriptomics

Proteomics

在蛋白质组学（Proteomics）数据分析中，缺失值是常见问题，解决缺失值的主要方法可以分为以下几类：

Single Value Replacement

单值替换

• 半最小值法（Half Minimum）
  • 将缺失值替换为所有观测数据中最小值的一半。
  • 适用场景：MNAR（Missing Not At Random，非随机缺失）。
• 均值替换（Mean）
  • 将缺失值替换为所有观测值的平均值。
  • 适用场景：MCAR/MAR（随机缺失/完全随机缺失）。

Global Structure Low-Rank Matrix Factorization

全局结构低秩矩阵分解

• PPCA（概率主成分分析）
  • 基于低秩的概率主成分分析方法插补缺失值。
  • 适用场景：MCAR/MAR。
• NIPALS（非线性迭代部分最小二乘法）
  • 通过低秩矩阵分解迭代估算缺失值。
  • 适用场景：MCAR/MAR。
• SVD（奇异值分解）
  • 通过低秩 SVD 矩阵分解进行插补，利用数据的全局结构。
  • 适用场景：MCAR/MAR。
• SVT（奇异值阈值化）
  • 通过核范数最小化方法解决缺失值问题，适用于低秩数据。
  • 适用场景：MCAR/MAR。

Local Similarity

局部相似性

• 样本最近邻（Sample-wise KNN）
  • 基于样本间的局部相似性，通过 kk-最近邻样本的加权平均值插补缺失值。
  • 适用场景：MAR（随机缺失）。
• 蛋白质最近邻（Protein-wise KNN）
  • 基于蛋白质之间的相似性，通过 kk-最近邻蛋白质的加权平均插补缺失值。
  • 适用场景：MAR（随机缺失）。

1. MNAR: 非随机缺失
   • 缺失值与未观测的数据本身有关，例如“半最小值法”。
2. MCAR: 完全随机缺失
   • 缺失值与观测数据无关，例如 PPCA、SVD、SVT 等矩阵分解方法。
3. MAR: 随机缺失
   • 缺失值与观测数据有关，但与未观测数据无关，例如 KNN 方法。

Single cell RNA-seq

• MAGIC
• scImpute
• SAVER
• ALRA
• SAUCIE

MAGIC

1. 原始数据 (Original Data)

• 输入是单细胞转录组的原始基因表达矩阵。
• 数据特点：由于技术限制，数据通常稀疏且有噪声。
• 可视化：点图展示了细胞在一个隐空间中的分布。

2. 计算距离矩阵 (Calculate Distances)

• 目的：计算细胞间的距离，基于基因表达值。
• 方法：
  • 使用欧几里得距离或其他距离度量。
• 结果：
  • 生成一个对称的距离矩阵，表示细胞两两之间的相似性。
  • 点图进一步展示细胞在空间中的连接趋势。

3. 计算亲和矩阵 (Calculate Affinities)

• 目的：将距离矩阵转化为亲和度矩阵（Affinity Matrix）。
• 方法：
  • 使用高斯核（Gaussian Kernel），将距离映射为亲和度。
  • 公式：$$Affinity\ = exp (-\frac{Distance^{2}}{2\sigma^{2}}) $$
• 结果：
  • 亲和度矩阵中，较小的距离对应高的亲和值，较大的距离对应低的亲和值。

4. 马尔科夫标准化 (Markov Normalization)

• 目的：对亲和度矩阵进行标准化，使其满足马尔科夫性质（每行和为1）。
• 方法：
  • 对矩阵进行归一化，得到马尔科夫过渡矩阵。
• 结果：
  • 生成的矩阵可用于模拟细胞间的扩散过程。

5. 马尔科夫矩阵指数化 (Exponentiate Markov Matrix)

• 目的：模拟扩散过程，扩散步数由参数 tt 决定。
• 方法：
  • 对马尔科夫矩阵进行 $t$ 次幂 $M^t$
• 效果：
  • 增加扩散步数 $t$ 可以加深数据的平滑程度，消除噪声。

6. 基因表达补全 (Impute Gene Expression)

• 计算：
  • 将扩散后的马尔科夫矩阵 $M^t$ 应用于原始数据矩阵 $D：Dimputed=Mt\cdot D{D}_{\text{imputed}}=M^t\cdot D$
  • 对补全后的数据进行重缩放。
• 结果：
  • 得到一个平滑且补全的基因表达矩阵，能够更好地反映生物学信号。

MAGIC 算法通过以下步骤实现数据补全：

1. 计算距离。
2. 转化为亲和度。
3. 使用马尔科夫模型模拟数据扩散。
4. 对基因表达进行平滑和补全。

这是一种有效的基于图的方法，可显著改善单细胞数据的解析质量。

Spatial Transcriptomics

• stDiff
• GNTD

stDiff

Matrix Dimension Reduction

Linear Methods

PCA

cMDS

Non-linear methods

• t-SNE
• UMAP
• KPCA
• mMDS
• Isomap
• LLE (Locally Linear Embedding)
• Laplacian Eigenmap

t-SNE

t-SNE（t-Distributed Stochastic Neighbor Embedding）是一种非线性降维技术，广泛用于高维数据的可视化。由 Laurens van der Maaten 和 Geoffrey Hinton 于 2008 年提出，t-SNE 能很好地保留数据的局部结构，因此特别适合于聚类或高维数据的可视化任务。

t-SNE 的基本原理

高维空间的相似度计算：

• 在高维空间中，t-SNE 用 高斯分布 表示点之间的相似性。

$$p_{ij}=\frac{\frac{exp(-||x_i-x_j|{|}^2)}{2{\sigma }_i^2}}{\sum _{k\ne i}exp(-||x_i-x_k|{|}^2)2{\sigma }_i^2}$$

• 其中，${\sigma }_i$ 是点 $i$ 的局部尺度参数，通过预定义的困惑度（Perplexity） 调整。

低维空间的相似度计算：

• 在低维空间中，点之间的相似性 $q_{ij}$ 用 学生分布（t-distribution） 表示：

$$q_{ij}=\frac{(1+||y_i-y_j|{|}^2{)}^{-1}}{\sum _{k\ne l}(1+||y_k-y_l|{|}^2{)}^{-1}}$$

这种分布的长尾特性使得低维空间更容易保留数据的局部结构。

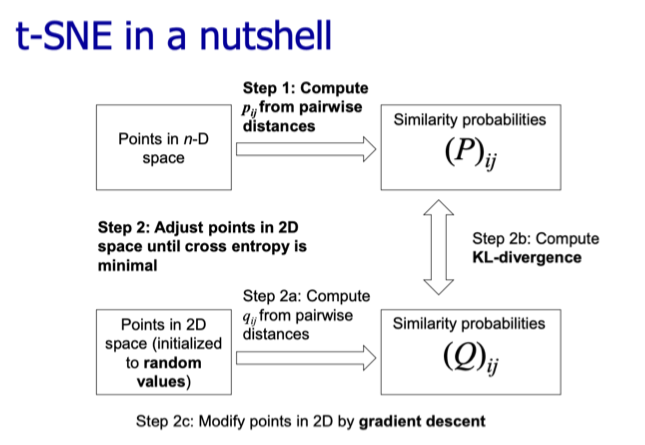
优化目标：

• t-SNE 的目标是使高维空间的相似性 $p_{ij}$ 和低维空间的相似性 $q_{ij}$ 尽可能接近。使用 Kullback-Leibler 散度（KL 散度）作为优化目标：

$$KL(P||Q)=\sum _i\sum _j{p}_{ij}log\frac{p_{ij}}{q_{ij}}$$

• 通过梯度下降算法最小化这个损失函数。

t-SNE 的核心参数

困惑度（Perplexity）：

• 用于平衡局部和全局结构的影响，通常值在 5 到 50 之间。
• 困惑度越高，模型关注的数据范围越大。

学习率（Learning Rate）：

• 对优化过程的速度和质量有较大影响。
• 通常建议的值为 200，但可以根据数据调整。

迭代次数：

• t-SNE 通常需要 1000 次以上的迭代才能收敛。

优点：

1. 非常适合用于高维数据的可视化。
2. 能很好地保留数据的局部结构，易于发现数据的聚类特性。

局限性：

1. 计算复杂度较高，不适合特别大规模的数据集。
2. 不适合用作一般降维算法（例如 PCA 的替代）。
3. 超参数（如困惑度、学习率）对结果影响较大，需要仔细调整。
4. 结果的随机性强，运行多次可能得到不同的结果。

UMAP

t-SNE converts the distance between the two points into a probability in an ad hoc manner and attempts to preserve this probability

UMAP, starts with a totally different idea: To construct a manifold from only a sampling of the points on it

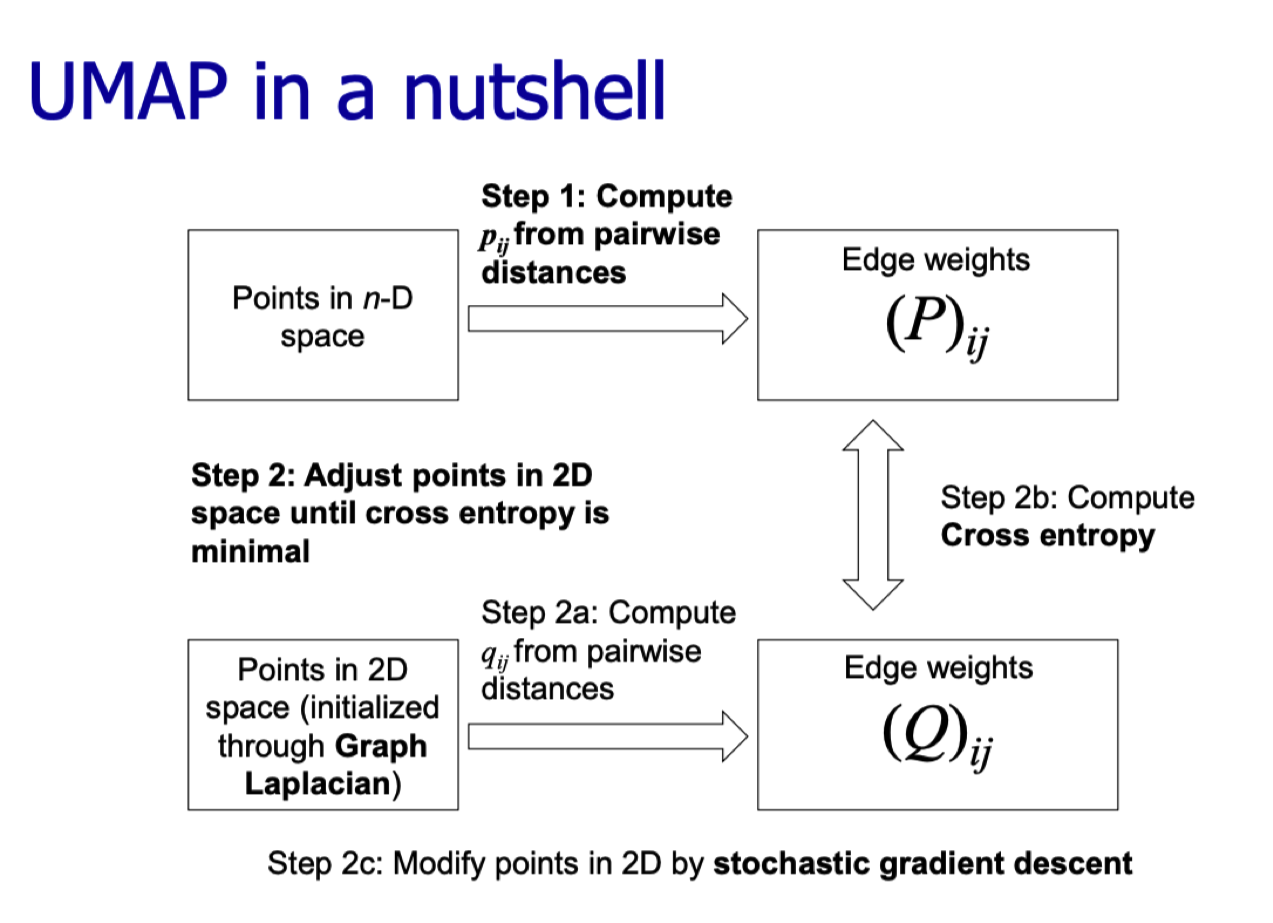
UMAP 的基本原理

UMAP 的理论基础是流形假设（Manifold Hypothesis），即高维数据在本质上分布在低维的流形上。UMAP 通过以下步骤实现降维：

构建高维空间的邻域图

• 计算邻居： 使用 k 近邻算法（k-NN）在高维空间中找到每个点的最近邻。
  • 用户需设置 n_neighbors 参数，决定邻域大小。
• 定义邻居相似度： 使用高斯分布计算邻域内点之间的相似性。

$$w_{ij}=exp(-\frac{||x_i-x_j||-{\rho }_i}{{\sigma }_i})$$

其中：

• $\rho$: 平滑参数，确保最近的邻居有较小的权重。

• ${\sigma }_i$：局部尺度参数，通过优化确保邻域结构的一致性。

• 生成一个加权无向图，点之间的权重代表相似性。

将高维邻域图嵌入到低维空间

• 在低维空间中，点之间的距离用一种**单调下降的曲线（通常是倒数函数）**来衡量。

$$d_{ij}=\frac{1}{1+a||y_i-y_j|{|}^{2b}}$$

其中 $a$ 和 $b$ 是超参数，通过优化选择，确保低维距离和高维相似性具有一致性。

• 优化目标是最小化高维邻域图和低维空间图之间的差异，使用交叉熵损失函数进行迭代优化。

优化过程

• UMAP 使用随机梯度下降（SGD）优化，将高维数据点映射到低维空间，同时保留高维数据的局部和全局结构。
• 与 t-SNE 不同，UMAP 的优化更高效，适用于大规模数据。

UMAP 的核心参数

1. n_neighbors（邻居数量）

   • 控制每个点的局部邻域大小，影响全局和局部结构的平衡。
   • 小值：强调局部结构。
   • 大值：保留更多全局结构。

2. min_dist（最小距离）

   • 控制嵌入空间中点之间的最小距离，影响聚类结果的紧密程度。
   • 小值：点簇更紧凑，聚类更明显。
   • 大值：点分布更稀疏。

3. n_components（降维后的维度）

   • 默认值为 2，适合可视化，但也可以设置为更高维度，用于特征提取或其他任务。

4. metric（距离度量）

   • 用于衡量高维空间中的点对相似性。默认是欧几里得距离，也支持其他距离（如曼哈顿距离、余弦相似度等）。

优点

1. 速度快：UMAP 的计算效率比 t-SNE 高，适合大规模数据。
2. 全局结构保留更好：UMAP 在降维时能同时保留局部和全局结构。
3. 参数可调性强：可以通过 n_neighbors 和 min_dist 调整对局部或全局结构的关注程度。
4. 适用范围广：支持多种距离度量，可应用于不同类型的数据（如图像、文本、基因数据）。

局限性

1. 参数较多，需要根据具体任务调整。
2. 对嵌入的随机性敏感，不同运行可能会有略微不同的结果。

UMAP 与 t-SNE 的比较

特性	UMAP	t-SNE
速度	更快，适合大规模数据	较慢，特别是大数据集时
全局结构	更好地保留全局结构	更关注局部结构
参数调节	更灵活，支持多种距离度量	参数少但对结果影响较大
嵌入稳定性	嵌入结果更稳定	嵌入结果具有一定随机性
使用场景	数据探索、聚类、降维	数据可视化（主要用于 2D 或 3D）

3D reconstruction from single cell RNA-seq