TOC-As-2

Question 1

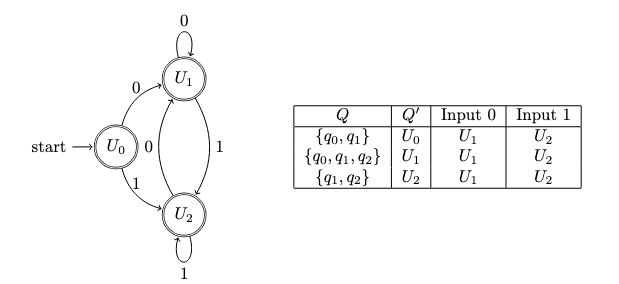
Convert the following NFA into an equivalent DFA. (20 pt)

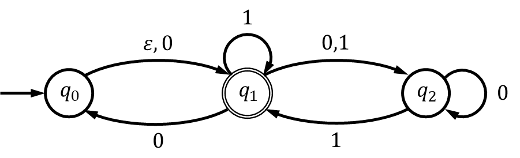
First iteration

• $U_0=E(q_0)=\{q_0,q_1\}$
• $move(U_0,0)=\{q_0,q_1,q_2\}$
• $E(move(U_0,0))=\{q_0,q_1,q_2\}=U_1$
• $move(U_0,1)=\{q_1,q_2\}$
• $E(move(U_0,0))=\{q_1,q_2\}=U_2$

Second iteration

• $move(U_1,0)=\{q_0,q_1,q_2\}$
• $E(move(U_1,0))=\{q_0,q_1,q_2\}=U_1$
• $move(U_1,1)=\{q_1,q_2\}$
• $E(move(U_1,1))=\{q_1,q_2\}=U_2$

Third iteration

• $move(U_2,0)=\{q_0,q_2\}$
• $E(move(U_2,0))=\{q_0,q_1,q_2\}=U_1$
• $move(U_2,1)=\{q_1,q_2\}$
• $E(move(U_2,1))=\{q_1,q_2\}=U_2$

$Q$	$Q^{\prime }$	$0$	$1$
$\{q_0,q_1\}$	$U_0$	$U_1$	$U_2$
$\{q_0,q_1,q_2\}$	$U_1$	$U_1$	$U_2$
$\{q_1,q_2\}$	$U_2$	$U_1$	$U_2$

Question 2

Let $\mathrm{\Sigma }=\{a,b\}$. Give a regular expression for each of the following language. (10 pt for each)

---

2.a. $L_1=\{a^n{b}^m|n\ge 4,m\le 3\}$.

$aaaa{a}^{\ast }(ϵ|b|bb|bbb)$

2.b. $L_2=\{w|wdoesnothaveaaaasasubstring\}$.

$(b|ab|aab{)}^{\ast }(ϵ|a|aa)$

---

Question 3

Determine whether the following languages over $\mathrm{\Sigma }=\{a,b\}$ are regular. Prove your answer. Each question has two languages. You don’t need to do both, select one at your favor. In general, the original languages are difficult, the alternative ones are easy. You have your own choice. If you do both, we mark the easy one. (10 pt for each subquestion)

3.a. $L_{3^{{}^{\prime }}}=\{a^n{b}^m{a}^n|n,m\in \mathbb{N}\}$

$L_{3^{{}^{\prime }}}$ is not regular.

Assume $L_{3^{{}^{\prime }}}$ is regular. Suppose $n=m=p$, Let $w=a^p{b}^p{a}^p$ , which is a string in $L_{3^{{}^{\prime }}}$

By the pumping lemma, $w$ is in the form $xyz$. The substring $y$ can be of the following three cases.

1. If $y$ only consists $a$'s

   • Suppose $y$ consists of $k$ $a^{\prime }s$.
     • Then $xyyz=a^{p+k}{b}^p{a}^p$ or $xyyz=a^p{b}^p{a}^{p+k}$
     • $p+k\ne p$, which is not in $L_{3^{{}^{\prime }}}$.

2. If $y$ only consists $b$'s

   • Suppose $y$ consists of $k$ $b^{\prime }s$.
     • Then $xyyz=a^p{b}^{k+p}{a}^p$
     • $k+p\ne p$, which is not in $L_{3^{{}^{\prime }}}$.

3. If $y$ consists both $a$'s and $b$'s

   • Then $a^{\prime }s$ and $b^{\prime }s$ in $xyyz$ are intersecting with each other, which is not in the form of $a^p{b}^p{a}^p$ Thus, $xyyz\notin L_{3^{{}^{\prime }}}$.

---

3.b. $L_4^{{}^{\prime }}=\{a^n{b}^m{a}^j|m>j\}$

$L_{4^{{}^{\prime }}}$ is not regular.

Assume $L_{4^{{}^{\prime }}}$ is regular. Suppose $j=p,m=n=p+1$, Let $w=a^{p+1}{b}^{p+1}{a}^p$ , which is a string in $L_{4^{{}^{\prime }}}$

By the pumping lemma, $w$ is in the form $xyz$. The substring $y$ can be of the following three cases.

1. If $y$ only consists of $a$'s

   • Suppose $y$ consists of $k$ $a^{\prime }s$.
     • Then $xyyz=a^{p+k+1}{b}^{p+1}{a}^p$ ,
       • $p+1+k\ne p+1$, which is not in $L_{4^{{}^{\prime }}}$.
     • Or $xyyz=a^{p+1}{b}^{p+1}{a}^{p+k}$
       • $p+k\ge p+1$, which is not in $L_{4^{{}^{\prime }}}$.

2. If $y$ only consists of $b$'s

   • Suppose $y$ consists of $k$ $b^{\prime }s$.
   • then $xyyz=a^{p+1}{b}^{p+1+k}{a}^p$
     • $p+1+k\ne p+1$, which is not in $L_{4^{{}^{\prime }}}$.

3. If $y$ consists of both $a$'s and $b$'s

   • Then $a^{\prime }s$ and $b^{\prime }s$ in $xyyz$ are intersecting with each other, which is not in the form of $a^p{b}^p{a}^p$ Thus, $xyyz\notin L_{4^{{}^{\prime }}}$.

---

3.c. $L_5^{{}^{\prime }}=\{a^n{b}^m{a}^j|m<n\vee m<j\}$

$L_{5^{{}^{\prime }}}$ is not regular.

Assume $L_{5^{{}^{\prime }}}$ is regular. Suppose $m=p$, $n=p+1,j=p+1$, Let $w=a^{p+1}{b}^p{a}^{p+1}$ , which is a string in $L_{5^{{}^{\prime }}}$

By the pumping lemma, $w$ is in the form $xyz$. The substring $y$ can be of the following three cases.

1. If $y$ only consists of $a$'s

   • Suppose $y$ consists of $k$ $a^{\prime }s$.
     • Then $xyyz=a^{p+1+k}{b}^p{a}^{p+1}$ ,
       • $p+1+k\ne p+1$, which is not in $L_{5^{{}^{\prime }}}$.
     • Or $xyyz=a^{p+1}{b}^p{a}^{p+1+k}$
       • $p+1+k\ge p+1$, which is not in $L_{5^{{}^{\prime }}}$.

2. If $y$ only consists of $b$'s

   • Suppose $y$ consists of $k$ $b^{\prime }s$.
     • Then $xyyz=a^{p+1}{b}^{p+k}{a}^{p+1}$
     • $p+k\ge p+1$, which is not in $L_{5^{{}^{\prime }}}$.

3. If $y$ consists of both $a$'s and $b$'s

   • Then $a^{\prime }s$ and $b^{\prime }s$ in $xyyz$ are intersecting with each other, which is not in the form of $a^p{b}^p{a}^p$ Thus, $xyyz\notin L_{5^{{}^{\prime }}}$.

---

3.d. $L_6^{{}^{\prime }}=\{a^n{b}^m|n\ge m\}\cup \{a^n{b}^m|m\ge n\}$

$L_{6^{{}^{\prime }}}$ is regular.

Since  $L_6\prime$  contains every possible string of  $a^n{b}^m$  (all strings with some number of  $a^{\prime }s$ followed by some number of  $b^{\prime }s$), this language is equivalent to:

$L_6\prime =\{a^n{b}^m\mid n,m\in \mathbb{N}\}$

Therefore, I can construct a NFA that accepts this language.

---

Question 4

Are the following languages regular? Prove your answer. (10 pt for each)

4.a. $L_7=\{a^n{b}^n|n\ge 1\}\cup \{a^n{b}^m|n\ge 1,m\ge 1\}$

$L_7$ is not regular.

$L_7$ can be divided into two parts. $\{a^n{b}^n|n\ge 1\}=L_9$ and $\{a^n{b}^m|n\ge 1,m\ge 1\}=L_{10}$

$L_9$ is not regular. Assume $L_9$ is regular. Suppose $n=p$, Let $w=a^p{b}^p$ , which is a string in $L_9$

By the pumping lemma, $w$ is in the form $xyz$. The substring $y$ can be of the following three cases.

1. If $y$ only consists of $a$'s

   • Suppose $y$ consists of $k$ $a^{\prime }s$.
     • Then $xyyz=a^{p+k}{b}^p$
     • $p+k\ne p$, which is not in $L_9$.

2. If $y$ only consists of $b$'s

   • Suppose $y$ consists of $k$ $b^{\prime }s$.
     • Then $xyyz=a^p{b}^{p+k}$
     • $k+p\ne p$, which is not in $L_9$.

3. If $y$ consists of both $a$'s and $b$'s

   • Then $a^{\prime }s$ and $b^{\prime }s$ in $xyyz$ are intersecting with each other, which is not in the form of $a^p{b}^p$ Thus, $xyyz\notin L_9$.

$L_{10}$ is regular, because $L_{10}=a^{+}{b}^{+}$

Although $L_{10}$ is regular, $L_7$ is the union of $L_9$ and $L_{10}$, and $L_9$ is not regular.
we can not construct a NFA for $L_7$. Thus, $L_7$ is not regular.

---

4.b. $L_8=\{a^n{b}^n|n\ge 1\}\cup \{a^n{b}^{n+2}|n\ge 1\}$

$L_8$ is not regular.

$L_8$ can be divided into two parts. $\{a^n{b}^n|n\ge 1\}$ and $\{a^n{b}^{n+2}|n\ge 1\}$. Let $L_9=\{a^n{b}^n|n\ge 1\}$ and $L_{11}=\{a^n{b}^{n+2}|n\ge 1\}$

$L_9$ is not regular, the proof has been shown in the previous question.

$L_{11}$ is not regular. Assume $L_{11}$ is regular. Suppose $n=p$, Let $w=a^p{b}^{p+2}$ , which is a string in $L_{11}$

By the pumping lemma, $w$ is in the form $xyz$. The substring $y$ can be of the following three cases.

1. If $y$ only consists of $a$'s

   • Suppose $y$ consists of $k$ $a^{\prime }s$.
     • Then $xyyz=a^{p+k}{b}^{p+2}$
     • $(p+2)-(p+k)\ne 2$, which is not in $L_{11}$.

2. If $y$ only consists of $b$'s

   • Suppose $y$ consists of $k$ $b^{\prime }s$.
     • Then $xyyz=a^p{b}^{p+2+k}$
     • $(p+2+k)-p\ne 2$, which is not in $L_{11}$.

3. If $y$ consists of both $a$'s and $b$'s

   • Then $a^{\prime }s$ and $b^{\prime }s$ in $xyyz$ are intersecting with each other, which is not in the form of $a^p{b}^{p+2}$ Thus, $xyyz\notin L_{11}$.

$L_9$ is not regular. $L_{11}$ is also not regular.

$L_8=L_9\cup L_{11}$ is not regular, we can not construct a NFA for $L_8$. Thus, $L_8$ is not regular.