Rasterization is the process of converting geometric data (like triangles) into pixels on a screen. It is a fundamental step in the graphics pipeline, where 3D models are transformed into 2D images.
CG-Rasterization
- Rasterizing a triangle
- Antialiasing
- Sampling theory
- Antialiasing in practice
- Visibility / occlusion
- Z-buffering
After MVP
Model transformation (placing objects)
View transformation (placing camera)
Projection transformation
- Orthographic projection (cuboid to "canonical" cube [-1, 113)
- Perspective projection (frustum to "canonical" cube)
Next: Rasterization (converting triangles to pixels)
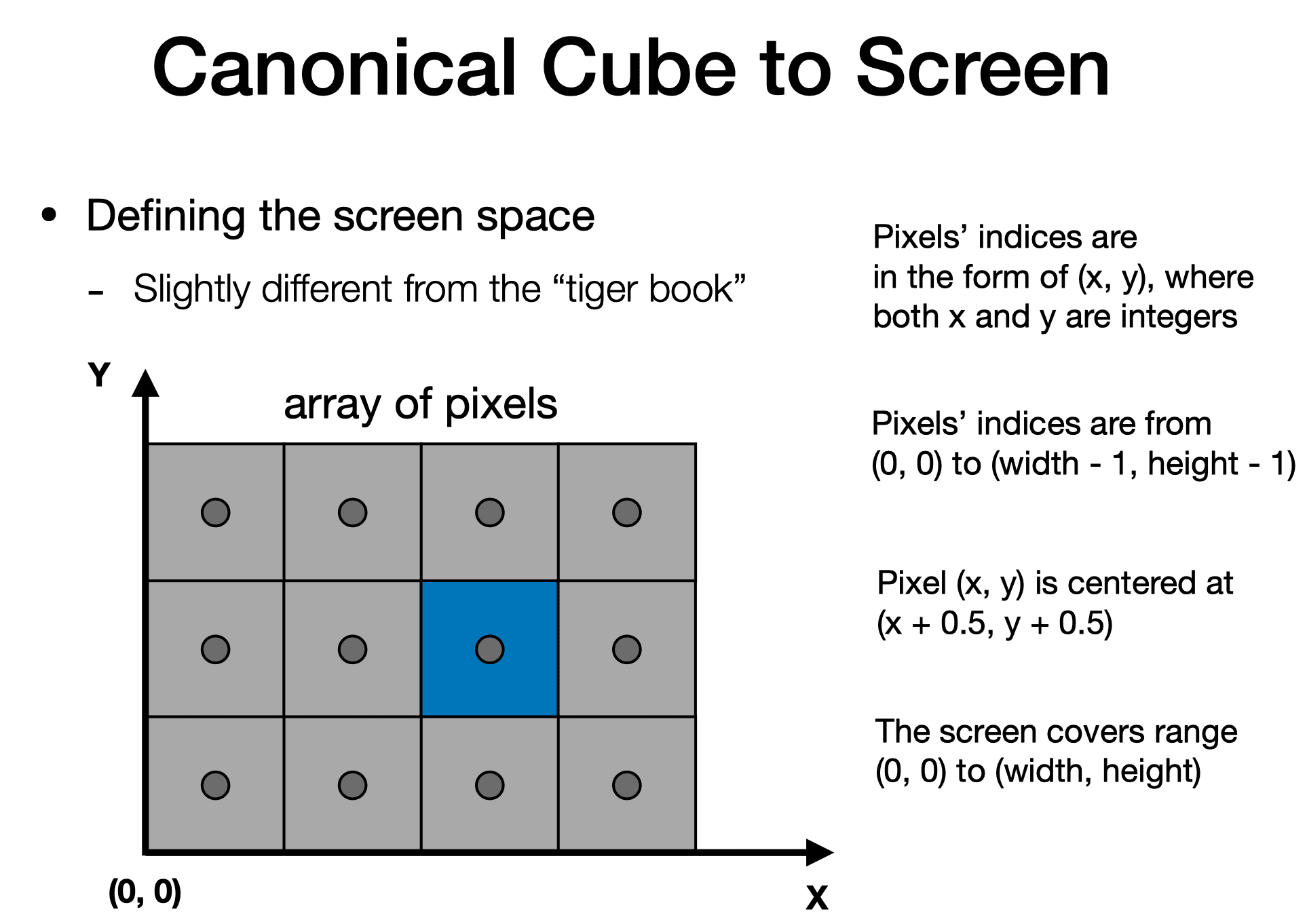
Canonical Cube to Screen
A screen:
- An array of pixels
- Size of the array: resolution
- A typical kind of raster display
Raster == Screen in German
- Rasterize == drawing onto the screen
Pixel (short for "picture element")
- For now: A pixel is a little square with uniform color
- Color is a mixture of (R,G,B)
Canonical Cube to Screen
- Irrelevant to
- Transform in xy plane
to - Viewport transformation matrix:
Triangles - Fundamental Shape Primitives
Why triangles?
Most basic polygon
- Break up other polygons
Unique properties
- Guaranteed to be planar
- Well-defined interior
- Well-defined method for interpolating values at vertices over triangle (barycentric interpolation)
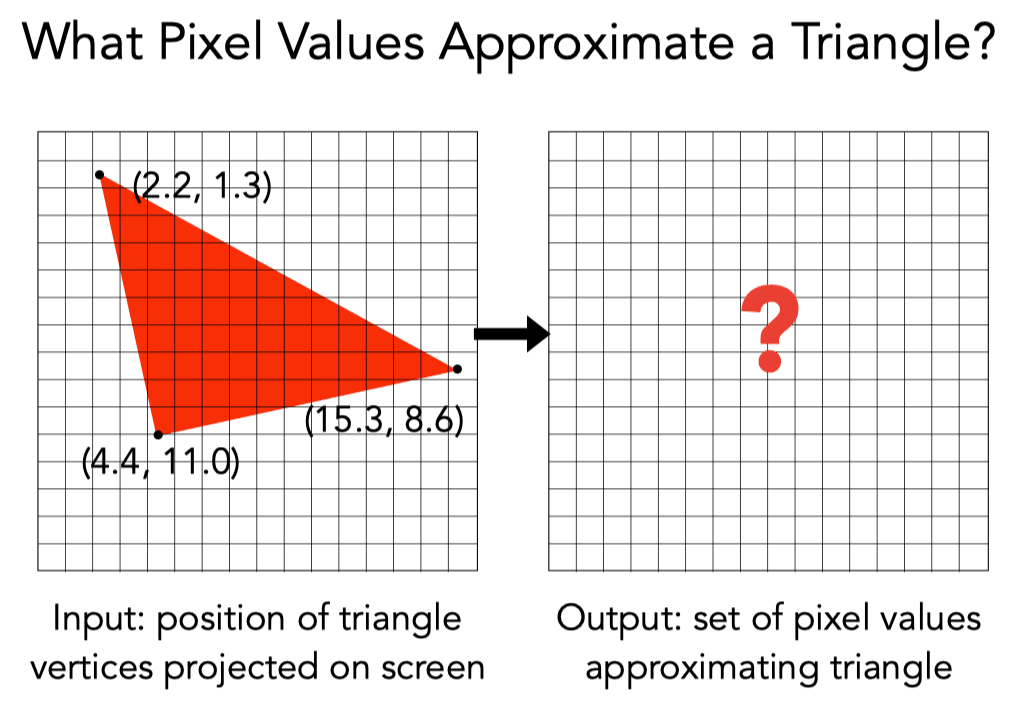
A Simple Approach: Sampling
Evaluating a function at a point is sampling.
We can discretize a function by sampling.
for (int x = 0; x < xmax; x++)
output[x]=f(x);Define Binary Function
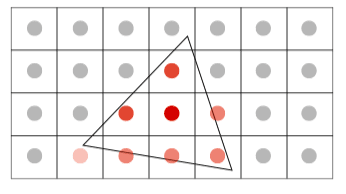
Rasterization = Sampling A 2D Indicator Function
for (int x = 0; x < xmax; x++)
for (int y = 0; y < ymax; y++)
output[x][y]=inside(tri,
x+0.5,
y+0.5);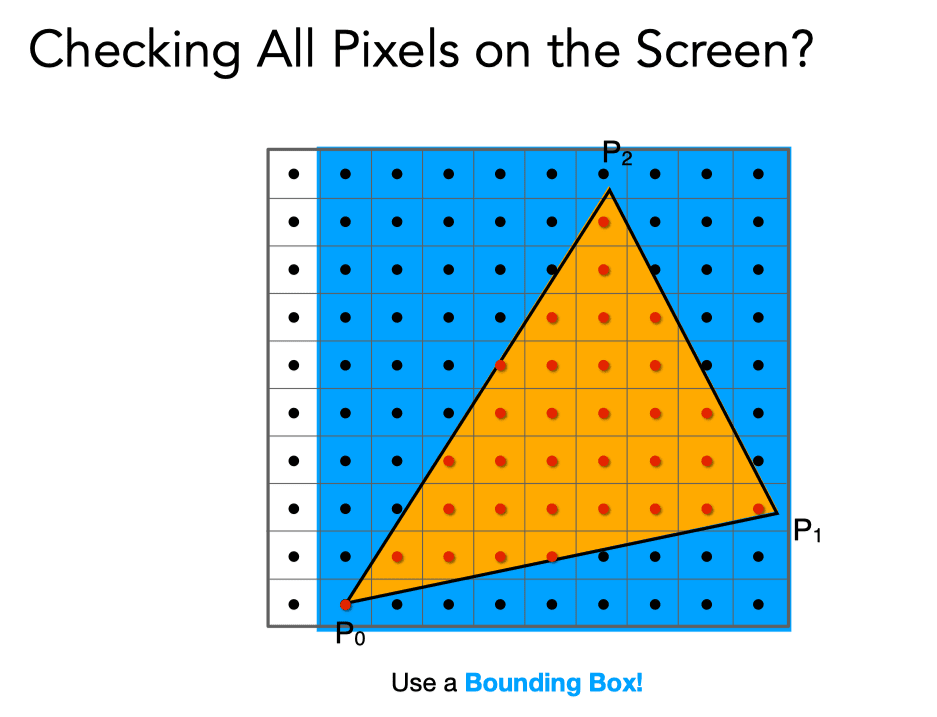 Access Aligned Bounding Box (AABB)
Access Aligned Bounding Box (AABB)
Sampling Artifacts
(Errors / Mistakes / Inaccuracies) in Computer Graphics
Artifacts due to sampling - "Aliasing"
- Jaggies - sampling in space
- Moire - undersampling images
- Wagon wheel effect - sampling in time
- [Many more] ...
Behind the Aliasing Artifacts
- Signals are changing too fast (high frequency), but sampled too slowly
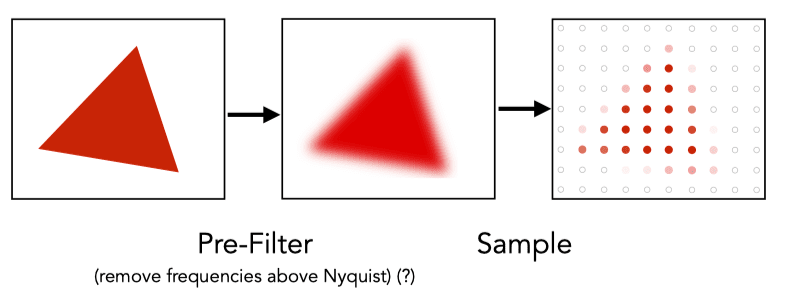
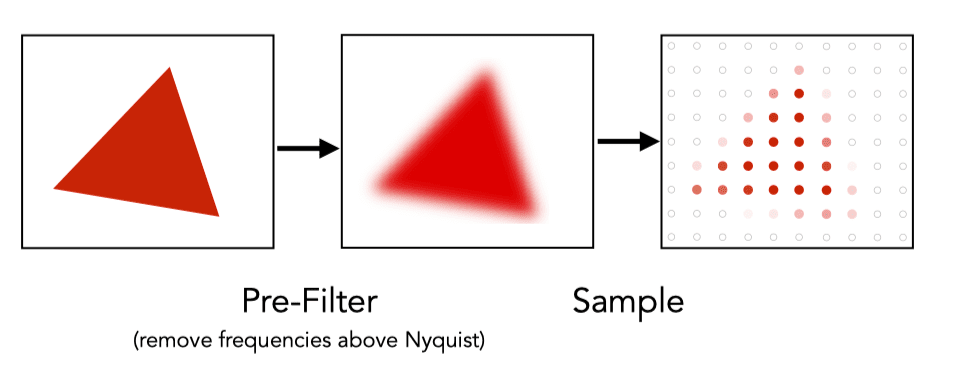
Antialiasing Idea: Blurring (Pre-Filtering) Before Sampling
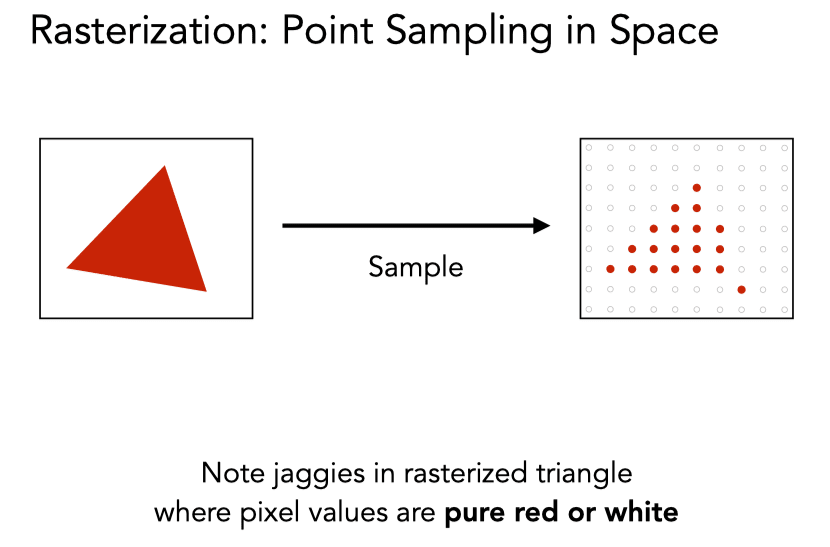
Rasterization: Antialiased sampling
Note antialiased edges in rasterized triangle where pixel values take intermediate values
Filter then Sample: Work Sample then Filter: Doesn't work
Why?
- Why undersampling introduces aliasing?
- Why pre-filtering then sampling can do antialiasing?
Filtering
Filtering - Getting rid of certain frequency contents
去掉一些频率的信息
Visualizing Image Frequency Content 
Filter Out Low Frequencies Only (Edges) 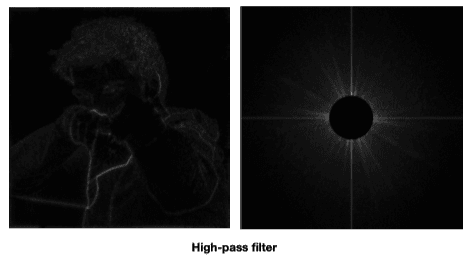
Filter Out High Frequencies (Blur) 
Filter Out Low and High Frequencies 
Filter Out Low and High Frequencies 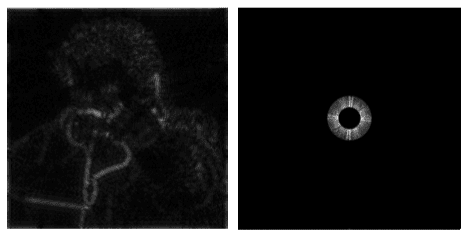
Filtering - Convolution (= Averaging)
Convolution Theorem
Convolution in the spatial domain is equal to multiplication,in the frequency domain, and vice versa
- Option 1:
- Filter by convolution in the spatial domain
- Option 2:
- Transform to frequency domain (Fourier transform)
- Multiply by Fourier transform of convolution kernel
- Transform back to spatial domain (inverse Fourier)
Box Function = "Low Pass" Filter

Wider Filter Kernel = Lower Frequencies

The larger the kernel, the photo will be more blurred, the lower the frequency.
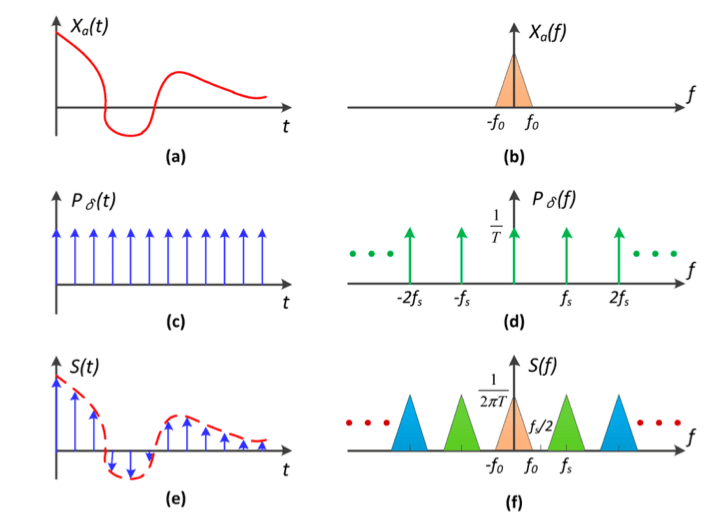
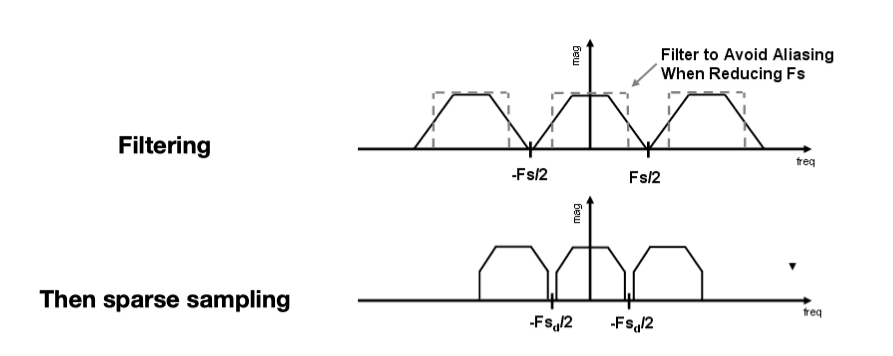
Sampling = Repeating Frequency Contents
Aliasing = Mixed Frequency Contents

How Can We Reduce Aliasing Error?
Option 1: Increase sampling rate
- Essentially increasing the distance between replicas in the Fourier domain
- Higher resolution displays, sensors, framebuffers...
- But: costly & may need very high resolution
Option 2: Antialiasing
- Making Fourier contents "narrower" before repeating
- i.e. Filtering out high frequencies before sampling
Antialiasing = Limiting, then repeating
Antialiased Sampling
Note antialiased edges in rasterized triangle where pixel values take intermediate values
A Practical Pre-Filter A 1 pixel-width box filter (low pass, blurring) before sampling

Antialiasing By Averaging Values in Pixel Area
Solution:
- Convolve f(x,y) by a 1-pixel box-blur
- Recall: convolving = filtering = averaging
- Then sample at every pixel's center
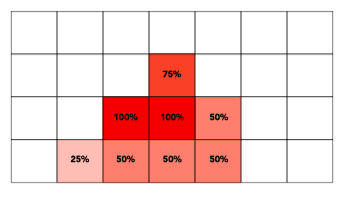
Antialiasing By Supersampling (MSAA)
Supersampling
Approximate the effect of the 1-pixel box filter by sampling multiple locations within a pixel and averaging their values
通过对像素内的多个位置进行采样并平均它们的值,来近似 1 像素框滤镜的效果
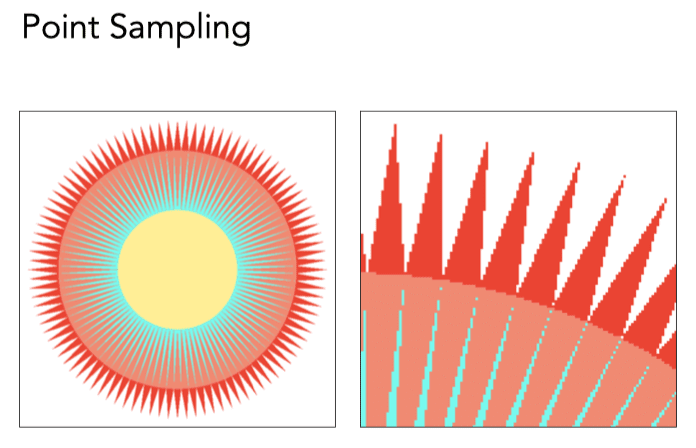
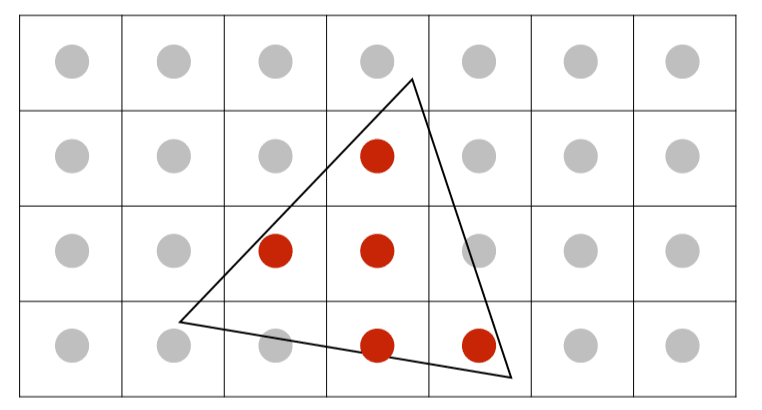
Point Sampling: One Sample Per Pixel
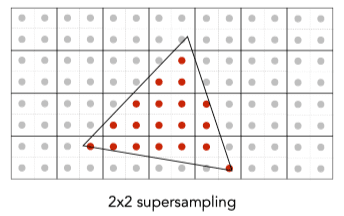
Supersampling
- Take NxN samples in each pixel.
- Average the NxN samples “inside” each pixel.
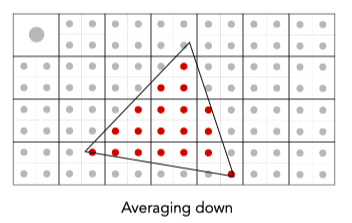
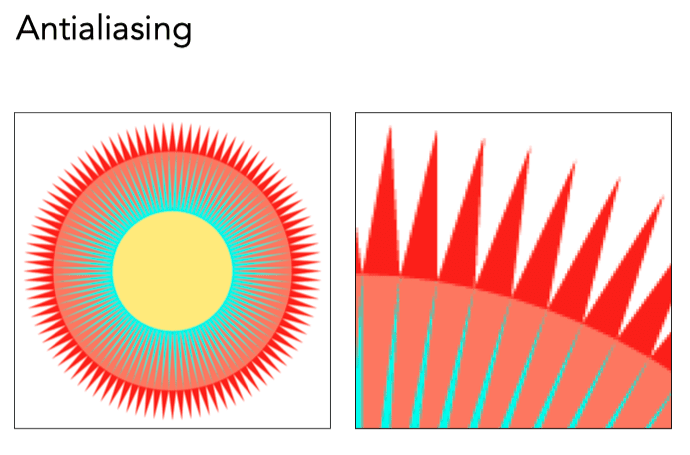
Antialiasing Today
Milestones (personal idea
- FXAA (Fast Approximate AA)
- Find edges, blur along edges
- TAA (Temporal AA)
- Antialiasing in time
Super resolution / super sampling
- From low resolution to high resolution
- Essentially still "not enough samples" problem
- DLSS (Deep Learning Super Sampling)