Assignment-1

$I$

1. Define what a Turing machine is.

   • Turing machine is the abstract model of all computers.
   • A Turing machine consists of a tape divided into cells, a moving read/write head, a state register storing the state of the Turing machine.

2. What is a UTM?

   • UTM is a Turing machine that could simulate all other Turing machines.

$II$

1. Describe the seven levels of transformations of a computer system.

• The seven levels of transformations in a computer system represent the progression from identifying a problem to the physical realization in a device. It starts with understanding the problem and formulating an algorithm, then translating it into a program. The program is mapped to an instruction set architecture, which is further implemented in a microarchitecture. At a lower level, the microarchitecture is translated into circuits, and finally, these circuits are realized in physical devices.

$III$

1. Explain the fetch-decode-execute cycle of the von Neumann Architecture.

   • the control unit fetch the next instruction from the memory
   • the instruction is decoded into a language that the ALU understands
   • data operands are fetched from the memory into the registers inside CPU
   • the ALU executes the instruction and places the result into the registers or memory

$IV$

1. Given 8 bits, represent the numbers +53 and -109 into binary using the following approach: 1) Signed-magnitude; 2) One’s complement; 3) Two’s complement.

• +53:
  1. Signed-magnitude: 00110101
  2. One’s complement: 00110101
  3. Two’s complement: 00110101
• -109
  1. Signed-magnitude: 11101101
  2. One’s complement: 10010010
  3. Two’s complement: 10010011

$V$

1. Convert -57.625 into binary using 32 bits floating number representation. Show your steps.

• -57.625 in binary using 32 bits floating number representation:
  • 1100 0010 0110 0110 1000 0000 0000 0000

$VI$

• Consider two hexadecimal numbers: x434F4D50 and x55544552. What values do they represent for each of the five data types shown?

	x434F4D50	x55544552
unsigned binary	0100 0011 0100 1111 0100 1101 0101 0000	0101 0101 0101 0100 0100 0101 0101 0010
1's complement	0100 0011 0100 1111 0100 1101 0101 0000	0101 0101 0101 0100 0100 0101 0101 0010
2's complement	0100 0011 0100 1111 0100 1101 0101 0000	0101 0101 0101 0100 0100 0101 0101 0010
$IEEE$ 754 floating point	207.302	$1.4587137\times {10}^{13}$
$ASCII$ string	COMP	UTER

$VII$

• The following Turing Machine is supposed to count in base 2. Fill in the missing rules.

{
   "name": "Binary Increment",
   "max_state": 25,
   "symbols": "xyzabc01$@",
   "tape": "100",
   "position": 2,
   "rules": [
      [ 0, "#", "1", 1, "R" ],
      [ 0, "0", "1", 1, "R" ],
      [ 0, "1", "0", 0, "L" ],
      [ 1, "#", "#", 0, "L" ],
      [ 1, "0", "0", 1, "R" ],
      [ 1, "1", "1", 1, "R" ]
   ]
}

$VIII$

• Show that $XZ=(X+Y)(X+\overline{Y})(\overline{X}+Z)$

• 1. Using truth table; (5 points)

$X$	$Y$	$Z$	$XZ$	$X+Y$	$X+\overline{Y}$	$\overline{X}+Z$	$(X+Y)(X+\overline{Y})(\overline{X}+Z)$
$T$	$T$	$T$	$T$	$T$	$T$	$T$	$T$
$T$	$T$	$F$	$F$	$T$	$T$	$F$	$F$
$T$	$F$	$T$	$T$	$T$	$T$	$T$	$T$
$T$	$F$	$F$	$F$	$T$	$T$	$F$	$F$
$F$	$T$	$T$	$F$	$T$	$F$	$T$	$F$
$F$	$T$	$F$	$F$	$T$	$F$	$T$	$F$
$F$	$F$	$T$	$F$	$F$	$T$	$T$	$F$
$F$	$F$	$F$	$F$	$F$	$T$	$T$	$F$

• 2. Using Boolean identities; (5 points)

$(X+Y)(X+\overline{Y})(\overline{X}+Z)$$=X(Y+\overline{Y})(\overline{X}+Z)$$=X(\overline{X}+Z)=(X\overline{X})+(XZ)=XZ$

$IX$

a. Write the Boolean expression in sum-of-products form.

• $\overline{X}\overline{Y}Z+\overline{X}Y\overline{Z}+X\overline{Y}Z+XY\overline{Z}$

b. Write the Boolean expression in product-of-sums form.

• $(X+Y+Z)(X+\overline{Y}+\overline{Z})(\overline{X}+Y+Z)(\overline{X}+\overline{Y}+\overline{Z})$

c. Simplify the sum-of-products form using Boolean identities;

• $\overline{X}\overline{Y}Z+\overline{X}Y\overline{Z}+X\overline{Y}Z+XY\overline{Z}$
• $=Y(\overline{X}\overline{Z}+X\overline{Z})+Z(\overline{X}\overline{Y}+X\overline{Y})$
• $=Y\overline{Z}+Z\overline{Y}$

d. Draw the logical circuit diagram for the simplified Boolean expression;

$X$

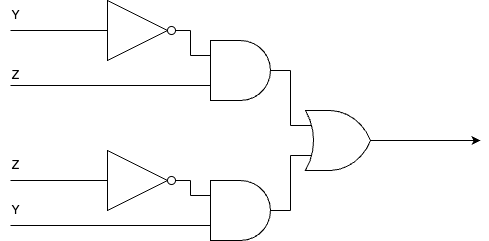
• Simplify the above Boolean expression using K-MAP.

	$\overline{X}\overline{Y}$	$X\overline{Y}$	$\overline{X}Y$	$XY$
$Z$	1	1	0	0
$\overline{Z}$	0	0	1	1

• $=Z\overline{Y}+\overline{Z}Y$