CSN & cCSN & PC

CSN

• CODE

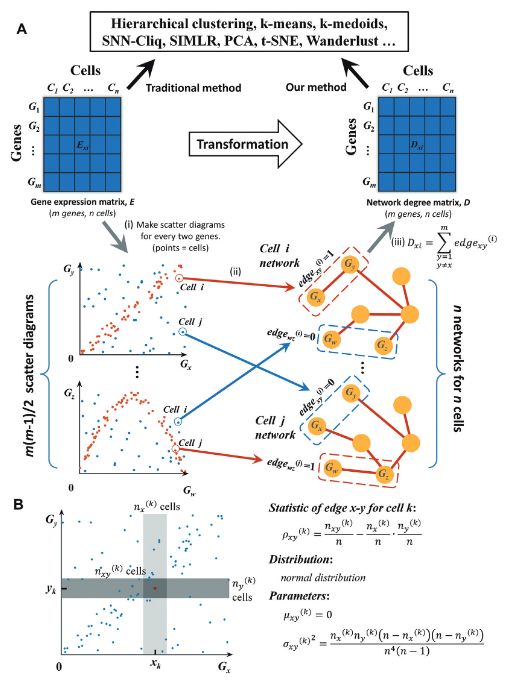
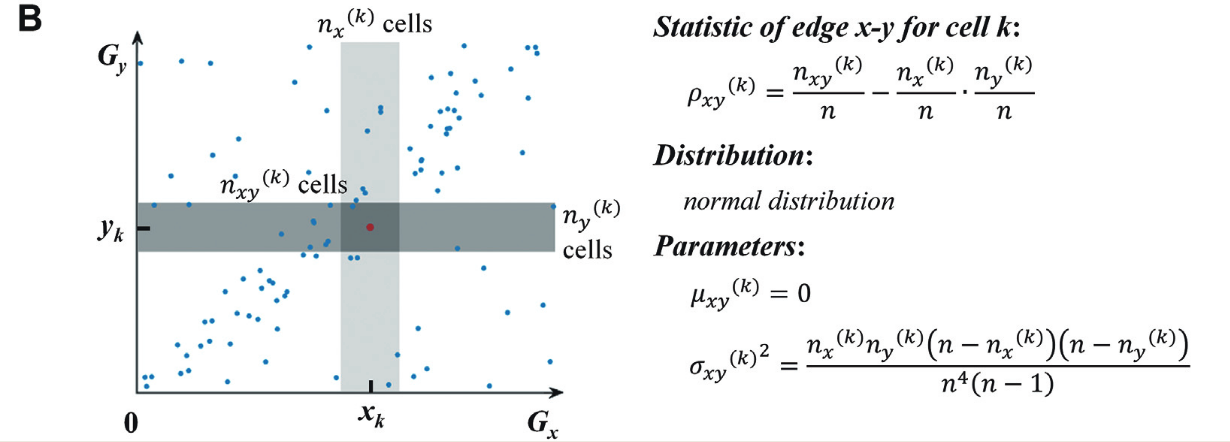
文章提出了一种基于统计依赖性的计算方法来构建每个细胞的基因-基因网络。

$p_x^{(k)}$ 和 $p_y^{(k)}$ 是单个基因的边缘概率，分别表示在单个细胞中基因 $x$ 和基因 $y$ 的表达概率。

$p_{x{y}^{(k)}}$ 是基因 $x$ 和基因 $y$ 在同一个细胞中的联合概率，表示这两个基因的联合表达概率。

• 对于每对基因 $x$ 和 $y$，定义一个新的统计量 ${\rho }_{xy}(k)$，用于度量它们在单个细胞 $k$ 中的独立性。这一统计量的计算过程基于概率的频率估算，具体步骤包括：
  • 计算每个基因的边缘频率 $p_x(x_k)$ 和 $p_y(y_k)$，这两者分别是基因 $x$ 和基因 $y$ 在细胞 $k$ 中的表达频率。
  • 计算基因对 $(x,y)$ 在细胞 $k$ 中的联合频率 $p_{xy}(x_k,y_k)$。

通过以下公式来估算这些概率：

边缘概率估算：

$$f_X(x_k)\approx \frac{n_x^{(k)}}{n},f_Y(y_k)\approx \frac{n_y^{(k)}}{n}$$

其中，$n_x^{(k)}$ 是在细胞 $k$ 附近的细胞中，基因 $x$ 表达量相近的细胞的个数。$n$ 是总的样本数。$n_y^{(k)}$也一样

$$f(x_k,y_k)\approx \frac{n_{x{y}^{(k)}}}{n}$$

可以得到每个细胞中基因对的独立性统计量 ${\rho }_{xy}(k)$，并根据其值来决定是否在特定细胞网络中连接这对基因。

PC

PC 算法的主要步骤如下：

1. 初始化阶段：首先，PC 算法假设所有的变量之间都有边相连，即它开始时认为每对变量之间都有可能存在直接的因果关系。

2. 独立性检验：然后，PC 算法通过对每对变量之间进行条件独立性检验来逐步删除图中的边。具体地，算法使用统计检验（如假设检验）来判断在控制其他变量的情况下，两个变量是否独立。如果独立，则表示这两个变量之间没有直接的因果关系，算法将删除该边。主要修改这部分代码

3. 逐步删除边：PC 算法采用逐步消除的策略，首先检测一对变量之间的边，然后逐渐增加控制的变量集合，直到无法进一步简化图结构。

4. 有向边与无向边：在完成边的删除后，PC 算法通过确定变量之间的条件独立性来确定哪些边应该是有向边。这个阶段通常需要额外的步骤来确定方向性，通常依赖于启发式规则和额外的假设（例如，假设数据来自于一个“真实”因果过程）。

5. 生成因果图：最后，PC 算法会输出一个因果结构图，图中的边表示变量之间可能的因果关系。

独立性检验

独立性

两个随机变量 $X$ 和 $Y$ 被认为是独立的，如果它们的联合分布等于它们各自的边缘分布的乘积。即：

$$P(X=x,Y=y)=P(X=x)\cdot P(Y=y)$$

换句话说，$X$ 和 $Y$ 不会互相影响，它们的出现是独立的。用概率的语言来说，$X$ 和 $Y$ 独立的条件是：

$$X\perp Y\text{if}P(X,Y)=P(X)P(Y)$$

条件独立性

条件独立性表示，在给定一个或多个变量的条件下，两个变量独立。用数学公式表示，如果给定了一个变量集合 $Z$，则$X$ 和 $Y$ 在条件集合 $Z$ 下是独立的，记作：

$$X\perp Y\mid Z$$

这意味着，在已知 $Z$ 的情况下，$X$ 和 $Y$ 之间没有依赖关系。用概率的语言表示条件独立性：

$$P(X,Y\mid Z)=P(X\mid Z)\cdot P(Y\mid Z)$$

即，条件独立性意味着，在条件 $Z$ 下，$X$ 和 $Y$ 的联合分布等于它们各自条件分布的乘积。

贝叶斯定理

贝叶斯定理可以用以下公式表示：

$$P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B)}=\frac{P(A\wedge B)}{P(B)}$$

其中：

• $P(A\mid B)$：在事件 $B$ 已经发生的条件下，事件 $A$ 发生的条件概率（后验概率）。
• $P(B\mid A)$：在事件 $A$ 已经发生的条件下，事件 $B$ 发生的条件概率（似然函数）。
• $P(A)$：事件 $A$ 发生的先验概率，表示在没有任何证据的情况下，事件 $A$ 发生的概率。
• $P(B)$：事件 $B$ 发生的总概率，可以通过全概率公式计算得到。

c-CSN

• CODE

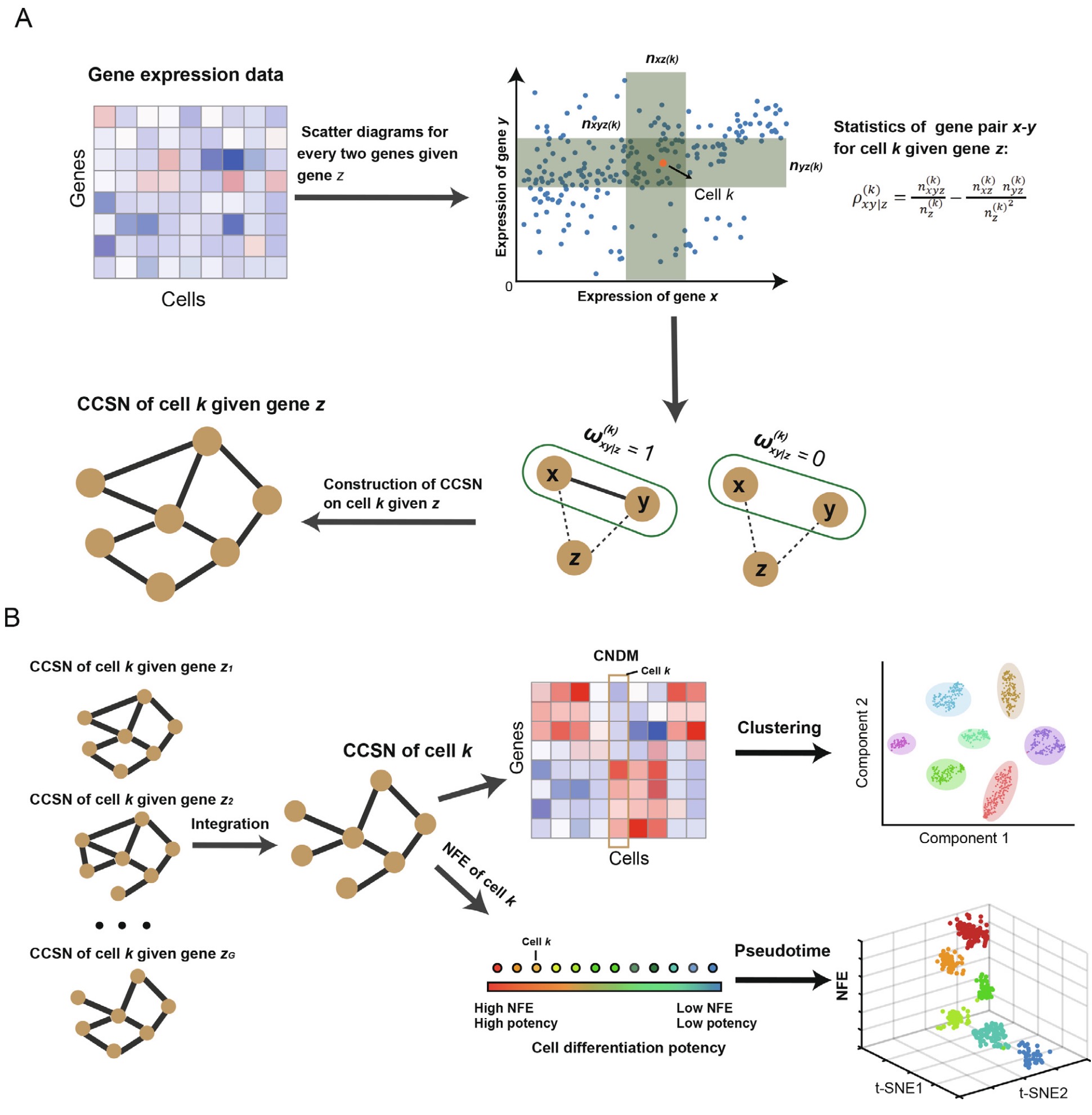
x, y 表示进行独立性检验的两个基因，Z 表示一个集合

根据条件独立性的定义

$$P(x_k,y_k\mid Z_k)=P(x_k\mid Z_k)\cdot P(y_k\mid Z_k)$$$$P(x_k,y_k\mid Z_k)=\frac{p(x{y}^{(k)}\wedge Z^{(k)})}{p_{Z^{(k)}}}=\frac{p(xy{Z}^{(k)})}{p_{Z^{(k)}}}=\frac{n_{xy{Z}^{(k)}}}{n_{Z^{(k)}}}$$$$P(x_k\mid Z_k)=\frac{p(x^{(k)}\wedge Z^{(k)})}{p_{Z^{(k)}}}=\frac{p(x{Z}^{(k)})}{p_{Z^{(k)}}}=\frac{n_{x{Z}^{(k)}}}{n_{Z^{(k)}}}$$$$P(y_k\mid Z_k)=\frac{p(y^{(k)}\wedge Z^{(k)})}{p_{Z^{(k)}}}=\frac{p(y{Z}^{(k)})}{p_{Z^{(k)}}}=\frac{n_{y{Z}^{(k)}}}{n_{Z^{(k)}}}$$$${\rho }_{{(xy|Z)}^{(k)}}=P(x_k,y_k\mid Z_k)-P(x_k\mid Z_k)\cdot P(y_k\mid Z_k)=\frac{n_{xy{Z}^{(k)}}}{n_{Z^{(k)}}}-\frac{n_{x{Z}^{(k)}}}{n_{Z^{(k)}}}\cdot \frac{n_{y{Z}^{(k)}}}{n_{Z^{(k)}}}$$$$=\frac{n_{xy{Z}^{(k)}}}{n_{Z^{(k)}}}-\frac{n_{x{Z}^{(k)}}\cdot n_{y{Z}^{(k)}}}{n_{Z^{(k)}}^2}$$